题目内容
12．已知{bn}首项为1，公差为$\frac{4}{3}$的AP，且a1+2a2+3a3+…+nan=$\frac{n（n+1）}{2}$•bn，求an．分析 通过{bn}首项为1，公差为$\frac{4}{3}$的AP，求出bn，利用已知条件求解an．
解答 解：{bn}首项为1，公差为$\frac{4}{3}$的AP，∴bn=1+$\frac{4}{3}$（n-1）=$\frac{4}{3}n-\frac{1}{3}$．
a1+2a2+3a3+…+nan=$\frac{n（n+1）}{2}$•bn，
可知：a1+2a2+3a3+…+（n-1）an-1=$\frac{n（n-1）}{2}$•bn-1，
∴nan=[$\frac{n（n+1）}{2}$]•bn-[$\frac{n（n-1）}{2}$]•bn-1=$\frac{n（n+1）}{2}$•$（\frac{4}{3}n-\frac{1}{3}）$-$\frac{n（n-1）}{2}$•$（\frac{4}{3}n-\frac{5}{3}）$，
解得an=2n-1．
点评 本题考查数列的通项公式的求法和前n项和的计算，解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
相关题目
3．在平面直角坐标系xOy中，以椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）上的一点A为圆心的圆与x轴相切于椭圆的一个焦点，与y轴相交于B，C两点，若△ABC是锐角三角形，则该椭圆的离心率的取值范围是（ ）
| A． | （$\frac{{\sqrt{6}-\sqrt{2}}}{2}$，$\frac{{\sqrt{5}-1}}{2}$） | B． | （$\frac{{\sqrt{6}-\sqrt{2}}}{2}$，1） | C． | （$\frac{{\sqrt{5}-1}}{2}$，1） | D． | （0，$\frac{{\sqrt{5}-1}}{2}$） |
如图，在海岸线EF一侧有一休闲游乐场，游乐场的前一部分边界为曲线段FGBC，该曲线段是函数y=Asin（ωx+ϕ）（A＞0，ω＞0，
如图，圆柱的轴截面ABCD是正方形，点E在底面的圆周上，BF⊥AE，F是垂足．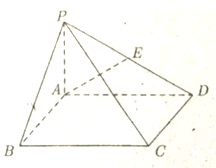
在四棱锥P-ABCD中，PA⊥底面ABCD，PA=1，底面ABCD是正方形，E是PD的中点，PD与底面ABCD所成的角为$\frac{π}{6}$，求异面直线AE与PC 所成的角的大小．