题目内容
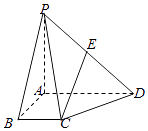
【题目】如图是市儿童乐园里一块平行四边形草地ABCD,乐园管理处准备过线段AB上一点E设计一条直线EF(点F在边BC或CD上,不计路的宽度),将该草地分为面积之比为2:1的左、右两部分,分别种植不同的花卉.经测量得AB=18m,BC=10m,∠ABC=120°.设EB=x,EF=y(单位:m). 
(1)当点F与C重合时,试确定点E的位置;
(2)求y关于x的函数关系式;
(3)请确定点E、F的位置,使直路EF长度最短.
【答案】
(1)解:∵S△BCE= ![]() ,SABCD=2×
,SABCD=2× ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴BE= ![]() AB=12.即E为AB靠近A的三点分点.
AB=12.即E为AB靠近A的三点分点.
(2)解:SABCD=18×10×sin120°=90 ![]() ,
,
当0≤x<12时,F在CD上,
∴SEBCF= ![]() (x+CF)BCsin60°=
(x+CF)BCsin60°= ![]() 90
90 ![]() ,解得CF=12﹣x,
,解得CF=12﹣x,
∴y= ![]() =2
=2 ![]() ,
,
当12≤x≤18时,F在BC上,
∴S△BEF= ![]() =
= ![]() ,解得BF=
,解得BF= ![]() ,
,
∴y= ![]() =
= ![]() ,
,
综上,y= 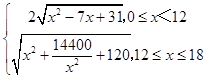 .
.
(3)解:当0≤x<12时,y=2 ![]() =2
=2 ![]() ≥5
≥5 ![]() ,
,
当12≤x≤18时,y= ![]() >
> ![]() >5
>5 ![]() ,
,
∴当x= ![]() ,CF=
,CF= ![]() 时,直线EF最短,最短距离为5
时,直线EF最短,最短距离为5 ![]() .
.
【解析】(1)根据面积公式列方程求出BE;(2)对F的位置进行讨论,利用余弦定理求出y关于x的解析式;(3)分两种情况求出y的最小值,从而得出y的最小值,得出E,F的位置.

 阅读快车系列答案
阅读快车系列答案【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)+B,A>0,ω>0,|φ|< ![]() 在某一个周期的图象时,列表并填入了部分数据,如表:
在某一个周期的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x | x1 |
| x2 |
| x3 |
Asin(ωx+φ)+B | 0 |
| 0 | ﹣ | 0 |
(1)请求出上表中的x1 , x2 , x3 , 并直接写出函数f(x)的解析式;
(2)若3sin2 ![]() ﹣
﹣ ![]() mf(
mf( ![]() ﹣
﹣ ![]() )≥m+2对任意x∈[0,2π]恒成立,求实数m的取值范围.
)≥m+2对任意x∈[0,2π]恒成立,求实数m的取值范围.