题目内容
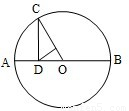
如图，圆O上一点C在直径AB上的射影为D．AD=2，AC=2| 5 |
10
10
，BC=4
| 5 |
4
．| 5 |
分析：由条件利用射影定理可得AC2=AD•AB，即 20=2•（BD+2），解得 BD的值，可得AB=BD+AD的值．再由BC2=BD•BA，求得 BC的值．
解答：解：圆O上一点C在直径AB上的射影为D．AD=2，AC=2
，则由射影定理可得AC2=AD•AB，即 20=2•（BD+2），
解得 BD=8，∴AB=2+BD=10．
再由BC2=BD•BA=8×10=80 可得 BC=4
，
故答案为 10；4
．
| 5 |
解得 BD=8，∴AB=2+BD=10．
再由BC2=BD•BA=8×10=80 可得 BC=4
| 5 |
故答案为 10；4
| 5 |
点评：本题主要考查射影定理的应用，三角形中的几何计算，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
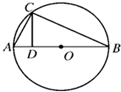
如图，圆O上一点C在直径AB上的射影为D．AD=2，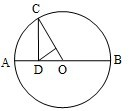
（2013•湖北）（选修4-1：几何证明选讲）
（几何证明选讲选做题）如图，圆O上一点C在直径AB上的射影为D，CD=4，BD=8，则圆O的半径等于
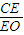的值为 ．