题目内容
（几何证明选讲选做题）如图，圆O上一点C在直径AB上的射影为D，CD=4，BD=8，则圆O的半径等于5
5
．分析：先由圆的性质得三角形ABC为直角三角形，再在直角三角形ACB中利用射影定理，计算AD的长，最后计算直径AB，从而得圆的半径
解答：解：∵圆O上一点C在直径AB上的射影为D
∴AC⊥BC，CD⊥AB
在直角三角形ACB中，由射影定理知：CD2=AD×BD
∵CD=4，BD=8
∴AD=
=
=2
∴AB=AD+DB=2+8=10
∴圆O的半径等于
=5
故答案为 5
∴AC⊥BC，CD⊥AB
在直角三角形ACB中，由射影定理知：CD2=AD×BD
∵CD=4，BD=8
∴AD=
| CD2 |
| BD |
| 42 |
| 8 |
∴AB=AD+DB=2+8=10
∴圆O的半径等于
| AB |
| 2 |
故答案为 5
点评：本题考查了圆的几何性质，直角三角形的射影定理及其应用，属基础题
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
（几何证明选讲选做题）
（几何证明选讲选做题）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，直线MN切⊙O于D，∠MDA=60°，则∠BCD=
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
（几何证明选讲选做题）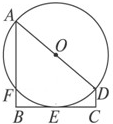
（几何证明选讲选做题）