题目内容
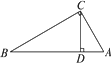
如图所示，已知CD是Rt△ABC的斜边AB上的高线，求证：CD·AC＝BC·AD．
答案：
解析：
解析：
|
证明：因为∠ACB＝90°，∠ADC＝90°， 因为∠A＋∠ACD＝90°，∠ACD＋∠BCD＝90°， 所以∠A＝∠BCD． 又因为∠ADC＝∠BDC， 所以△ADC∽△CDB． 所以CD∶BC＝AD∶AC，即CD·AC＝BC·AD． 分析：把等积式转化为比例式CD∶BC＝AD∶AC，再通过三角形相似得证． |
练习册系列答案
阅读快车系列答案
相关题目
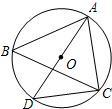
如图所示，已知⊙O是△ABC的外接圆，AD是⊙O的直径，连接CD，若AD=3，AC=2，则cosD的值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
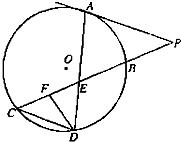如图所示，已知PA是⊙O相切，A为切点，PBC为割线，弦CD∥AP，AD、BC相交于E点，F为CE上一点，且DE2=EF•EC．
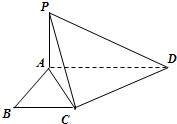如图所示，已知ABCD是直角梯形，∠ABC=90°，AD∥BC，AD=2，AB=BC=1，PA⊥平面ABCD．
