Question

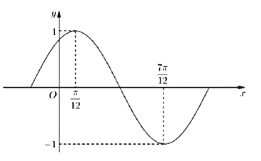
【题目】函数 部分图象如图所示.

（1）求的最小正周期及解析式；

（2）设，求函数在区间上的最大值和最小值.

Answer 1

【答案】（1） ,；（2）在区间上的最大值为，最小值为．

【解析】

（1）由图可知A＝1，，从而可求ω；再由图象经过点（，1），可求得；

（2）依题意g（x）化简整理为g（x）＝sin（2x），再利用正弦函数的性质结合x的范围求得g（x）的最大值和最小值．

（1）由图可知：，A＝1，

∴T＝π，

∴ω2，

∴f（x）＝cos（2x+）

又∵图象经过点，

∴1＝cos（2），

∴2kπ，k∈Z，

∴2kπ，k∈Z，

又∵||，

∴，

∴解析式为f（x）＝cos（2x）；

（2）g（x）＝f（x）+sin2x

＝cos（2x）+sin2x

＝cos2xcossin2xsin

sin2xcos2x

＝sin（2x）；当时，2x，

当2x时，即x=时，g（x）的最大值为，当2x，即x=时g（x）的最小值为，

综上所述，在区间上的最大值为，最小值为．