题目内容
已知函数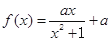 ,
,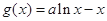 (
(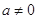 ).
).
(1)求函数 的单调区间;
的单调区间;
(2)求证:当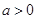 时,对于任意
时,对于任意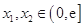 ,总有
,总有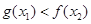 成立.
成立.
(1)当 时,
时, 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 ,
, ;当
;当 时,
时, 的单调递增区间为
的单调递增区间为 ,
, ,单调递减区间为
,单调递减区间为 ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)对于含参数的函数的单调区间,只需在定义域内考虑导函数符号,同时要注意分类讨论标准的确定.先求 ,分母恒正,只需考虑分子二次函数的符号,所以讨论开口方向即可;(2)由于
,分母恒正,只需考虑分子二次函数的符号,所以讨论开口方向即可;(2)由于 是独立的两个变量,故
是独立的两个变量,故 分别代表
分别代表 ,
, 的任意两个函数值,要使得
的任意两个函数值,要使得 恒成立,只需证明
恒成立,只需证明 ,分别利用导数求其最大值和最小值,从而得证,该题入手,可能很多同学困惑于
,分别利用导数求其最大值和最小值,从而得证,该题入手,可能很多同学困惑于 这两个变量的处理,从而造成了解题障碍.
这两个变量的处理,从而造成了解题障碍.
试题解析:(Ⅰ)函数 的定义域为
的定义域为 ,
, .
.
当 时,
时,
当 变化时,
变化时, ,
, 的变化情况如下表:
的变化情况如下表:
当







0 
0 

↘ ↗ ↘  时,
时,
当 变化时,
变化时, ,
, 的变化情况如下表:
的变化情况如下表:
 练习册系列答案
练习册系列答案
名师特攻百分好题测评卷系列答案
单元加期末100分冲刺卷系列答案
单元月考期末测评卷系列答案
新课堂单元测试卷系列答案
钟书金牌一卷夺冠系列答案

名师优选冲刺卷系列答案
创新学习同步解析与测评系列答案
高效同步测练系列答案
王朝霞考点梳理时习卷系列答案
相关题目
 上的函数
上的函数 同时满足以下条件:
同时满足以下条件: 在(0,1)上是减函数,在(1,+∞)上是增函数;
在(0,1)上是减函数,在(1,+∞)上是增函数; 是偶函数;
是偶函数; y=x+2垂直.
y=x+2垂直. =
= ,若存在实数x∈[1,e],使
,若存在实数x∈[1,e],使 <
< 在
在 及
及 时取得极值.
时取得极值. ,都有
,都有 成立,求c的取值范围.
成立,求c的取值范围. .
. 的单调性;
的单调性; 在(1,+
在(1,+ )恒成立,求实数a的取值范围.
)恒成立,求实数a的取值范围. R
R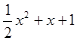 有唯一公共点;
有唯一公共点;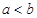 ,比较
,比较 与
与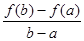 的大小,并说明理由。
的大小,并说明理由。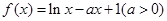 。
。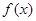 的零点个数;
的零点个数; 轴交于
轴交于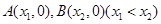 两点,
两点,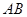 中点为
中点为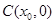 ,设函数
,设函数 , 求证:
, 求证: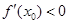 。
。 (k为常数,e=2.71828……是自然对数的底数),曲线
(k为常数,e=2.71828……是自然对数的底数),曲线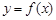 在点
在点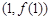 处的切线与x轴平行。
处的切线与x轴平行。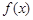 的单调区间;
的单调区间;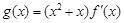 ,其中
,其中 为
为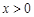 ,
, 。
。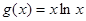 .
.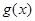 在
在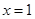 处的切线方程;
处的切线方程;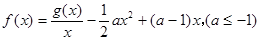 的单调区间;
的单调区间; ,求证:
,求证: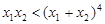 .
.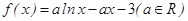 .
. ,求函数
,求函数 的单调区间;
的单调区间;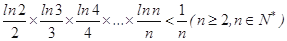
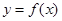 的图象在点
的图象在点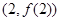 处的切线的倾斜角为
处的切线的倾斜角为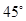 ,对于任意的
,对于任意的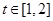 ,函数
,函数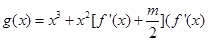 是
是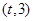 上总不是单调函数,求
上总不是单调函数,求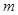 的取值范围。
的取值范围。