题目内容
已知函数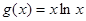 .
.
(Ⅰ)求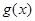 在
在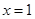 处的切线方程;
处的切线方程;
(Ⅱ)求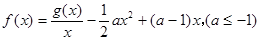 的单调区间;
的单调区间;
(Ⅲ)若 ,求证:
,求证: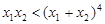 .
.
(Ⅰ) ;(Ⅱ)当
;(Ⅱ)当 ,
,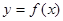 的单调增区间
的单调增区间 ;当
;当 时,函数
时,函数 的单调递增区间是
的单调递增区间是 ,单调递减区间是
,单调递减区间是 ;(Ⅲ)详见解析.
;(Ⅲ)详见解析.
解析试题分析:(Ⅰ)求出导数及切点,利用直线的点斜式方程即可得切线方程.
(Ⅱ)将 求导,利用
求导,利用 求得其递增区间,
求得其递增区间, 求得其递减区间.
求得其递减区间.
在本题中, ,由
,由 得:
得: .当
.当 ,
, 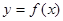 的单调增区间
的单调增区间 ;
;
当 时,函数
时,函数 的单调递增区间是
的单调递增区间是 ,单调递减区间是
,单调递减区间是 .
.
(Ⅲ)本题首先要考虑的是,所要证的不等式与函数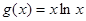 有什么关系?待证不等式可做如下变形:
有什么关系?待证不等式可做如下变形:  ,最后这个不等式与
,最后这个不等式与 有联系吗?我们往下看.
有联系吗?我们往下看. ,所以在
,所以在 上
上 是增函数.
是增函数.
因为 ,所以
,所以
即 从这儿可以看出,有点联系了.同理
从这儿可以看出,有点联系了.同理 ,
,
所以 ,
,
与待证不等式比较,只要 问题就解决了,而这由重要不等式可证,从而问题得证.
问题就解决了,而这由重要不等式可证,从而问题得证.
试题解析:(Ⅰ) ,
, ,所以切线为:
,所以切线为: 即
即 3分
3分
(Ⅱ) ,
, , 4分
, 4分 ,
, , 5分
, 5分
当 ,
,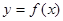 的单调增区间
的单调增区间 ; 6分
; 6分
当 时,函数
时,函数 的单调递增区间是
的单调递增区间是 ,单调递减区间是
,单调递减区间是 . 8分
. 8分
(Ⅲ) ,所以在
,所以在 上
上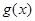 是增函数,
是增函数,  上是减函数
上是减函数
因为 ,所以
,所以
即 ,同理
,同理 .
.
所以
又因为 当且仅当“
当且仅当“ ”时,取等号.
”时,取等号.
又 ,
, ,
,
所以 ,所以
,所以 ,
,
所以: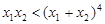 . 14分
. 14分
考点:1、导数的应用;2、不等式的证明.

练习册系列答案
相关题目
 ,
, ,
, ,其中
,其中 ,且
,且 .
. 时,求函数
时,求函数 的最大值;
的最大值; 的单调区间;
的单调区间; 若对任意给定的非零实数
若对任意给定的非零实数 ,存在非零实数
,存在非零实数 (
( ),使得
),使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.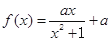 ,
,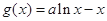 (
(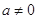 ).
). 的单调区间;
的单调区间;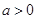 时,对于任意
时,对于任意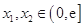 ,总有
,总有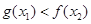 成立.
成立. ,其中a>0.
,其中a>0. 的单调区间;
的单调区间; 是曲线
是曲线 的切线,求实数a的值;
的切线,求实数a的值; ,求
,求 在区间
在区间 上的最大值(其中e为自然对的底数)。
上的最大值(其中e为自然对的底数)。 亿元,其中用于风景区改造为
亿元,其中用于风景区改造为 亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用
亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用 亿元,至多
亿元,至多 亿元;③每年用于风景区改造费用
亿元;③每年用于风景区改造费用 ,
, ,请你分析能否采用函数模型y=
,请你分析能否采用函数模型y=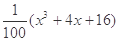 作为生态环境改造投资方案.
作为生态环境改造投资方案.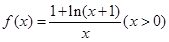
 在区间
在区间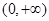 上是增函数还是减函数?证明你的结论;
上是增函数还是减函数?证明你的结论;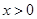 时,
时,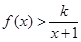 恒成立,求整数
恒成立,求整数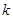 的最大值;
的最大值;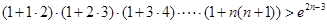
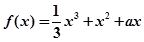 .
. 在区间
在区间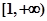 单调递增,求
单调递增,求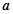 的最小值;
的最小值;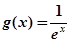 ,对
,对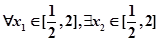 ,使
,使 成立,求
成立,求 的范围.
的范围.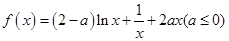 .
.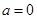 时,求
时,求 的极值;(2)当
的极值;(2)当 时,讨论
时,讨论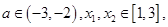 恒有
恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围. 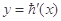 的图象如图,f(x)=6lnx+h(x)
的图象如图,f(x)=6lnx+h(x)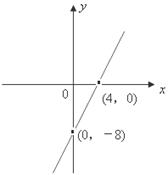
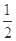 )上是单调函数,求实数m的取值范围;
)上是单调函数,求实数m的取值范围;