题目内容
3.已知定义在R上的偶函数f(x)满足f(x-4)=f(x),且在区间[0,2]上f(x)=x,若关于x的方程f(x)=loga|x|有六个不同的根,则a的范围为( )| A. | ($\sqrt{6}$,$\sqrt{10}$) | B. | ($\sqrt{6}$,2$\sqrt{2}$) | C. | (2,2$\sqrt{2}$) | D. | (2,4) |
分析 首先求出f(x)的周期是4,画出函数的图象,得到关于a的不等式,解得即可.
解答 解:由f(x-4)=f(x)可得周期等于4,
当x∈(0,10]时,函数的图象如图
f(2)=f(6)=f(10)=2,
再由关于x的方程f(x)=loga|x|有六个不同的根,则关于x的方程f(x)=logax有三个不同的根,
可得$\left\{\begin{array}{l}{lo{g}_{a}6<2}\\{lo{g}_{a}10>2}\end{array}\right.$,
解得 a∈($\sqrt{6}$,$\sqrt{10}$),
故选A.
点评 本题主要考查函数的图象特征,体现了数形结合的数学思想,属于中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
13.设点P为公共焦点F1(-2,0),F2(2,0)的椭圆和双曲线的一个交点,且cos∠F1PF2=$\frac{3}{5}$,已知椭圆的长轴长是双曲线实轴长的4倍,则双曲线的离心率为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
11.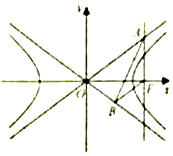 如图,已知双曲线$C:\frac{x^2}{a^2}-{y^2}=1(a>0)$的右焦点F,点A,B分别在C的两条渐近线上,AF⊥x轴,AB⊥OB,BF∥OA(O为坐标原点).求双曲线C的方程.
如图,已知双曲线$C:\frac{x^2}{a^2}-{y^2}=1(a>0)$的右焦点F,点A,B分别在C的两条渐近线上,AF⊥x轴,AB⊥OB,BF∥OA(O为坐标原点).求双曲线C的方程.
 如图,已知双曲线$C:\frac{x^2}{a^2}-{y^2}=1(a>0)$的右焦点F,点A,B分别在C的两条渐近线上,AF⊥x轴,AB⊥OB,BF∥OA(O为坐标原点).求双曲线C的方程.
如图,已知双曲线$C:\frac{x^2}{a^2}-{y^2}=1(a>0)$的右焦点F,点A,B分别在C的两条渐近线上,AF⊥x轴,AB⊥OB,BF∥OA(O为坐标原点).求双曲线C的方程.
15.设全集U={1,2,3,4,5,6,7},B={2,4,6},则∁UB=( )
| A. | {2,4,6} | B. | {1,3,5} | C. | {1,3,5,7} | D. | {1,3} |
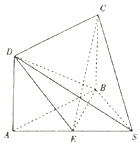 如图,在四棱锥S-ABCD中,四边形为ABCD矩形,E为SA的中点,SA=SB,AB=2$\sqrt{3}$,BC=3.
如图,在四棱锥S-ABCD中,四边形为ABCD矩形,E为SA的中点,SA=SB,AB=2$\sqrt{3}$,BC=3.