题目内容
已知向量 =(
=( sin
sin ,1),
,1), =(cos
=(cos ,cos2
,cos2 ),函数f(x)=
),函数f(x)= .
.
(1)若f(x)=1,求cos( -x)的值;
-x)的值;
(2)在△ABC中,角A,B,C的对边分别是a,b,c,且满足acosC+ c=b,求f(B)的取值范围.
c=b,求f(B)的取值范围.
解:(1)由题意得:函数f(x)= =
=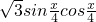 +
+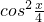 =
= +
+ =sin(
=sin( )+
)+ .
.
若 f(x)=1,可得 sin( )=
)= ,
,
则 cos( -x)=2
-x)=2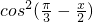 -1=2
-1=2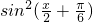 -1=-
-1=- .
.
(2)由acosC+ c=b可得 a•
c=b可得 a• +
+ c=b,即 b2+c2-a2=bc.
c=b,即 b2+c2-a2=bc.
∴cosA= =
= ,∴A=
,∴A= ,B+C=
,B+C= .
.
∴0<B< ,0<
,0< <
< ,
,
∴ <
<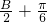 <
< ,
, <sin(
<sin( 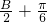 )<1,
)<1,
∴f(B)=sin(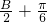 )+
)+ ∈(1,3).
∈(1,3).
分析:(1)利用两个向量的数量积公式求得函数f(x)=sin( )+
)+ ,由 f(x)=1,可得 sin(
,由 f(x)=1,可得 sin( )=
)= ,再利用二倍角公式求得cos(
,再利用二倍角公式求得cos( -x)的值.
-x)的值.
(2)由acosC+ c=b利用余弦定理可得 cosA=
c=b利用余弦定理可得 cosA= =
= ,求出 A=
,求出 A= ,B+C=
,B+C= .再由
.再由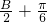 的范围求出f(B)=sin(
的范围求出f(B)=sin(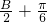 )+
)+ 的范围.
的范围.
点评:本题主要考查两个向量的数量积公式的应用,余弦定理和诱导公式、二倍角公式的应用,正弦函数的定义域和值域,属于中档题.
 =
=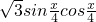 +
+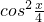 =
= +
+ =sin(
=sin( )+
)+ .
.若 f(x)=1,可得 sin(
 )=
)= ,
,则 cos(
 -x)=2
-x)=2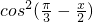 -1=2
-1=2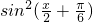 -1=-
-1=- .
.(2)由acosC+
 c=b可得 a•
c=b可得 a• +
+ c=b,即 b2+c2-a2=bc.
c=b,即 b2+c2-a2=bc.∴cosA=
 =
= ,∴A=
,∴A= ,B+C=
,B+C= .
.∴0<B<
 ,0<
,0< <
< ,
,∴
 <
<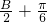 <
< ,
, <sin(
<sin( 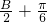 )<1,
)<1,∴f(B)=sin(
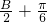 )+
)+ ∈(1,3).
∈(1,3).分析:(1)利用两个向量的数量积公式求得函数f(x)=sin(
 )+
)+ ,由 f(x)=1,可得 sin(
,由 f(x)=1,可得 sin( )=
)= ,再利用二倍角公式求得cos(
,再利用二倍角公式求得cos( -x)的值.
-x)的值.(2)由acosC+
 c=b利用余弦定理可得 cosA=
c=b利用余弦定理可得 cosA= =
= ,求出 A=
,求出 A= ,B+C=
,B+C= .再由
.再由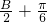 的范围求出f(B)=sin(
的范围求出f(B)=sin(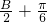 )+
)+ 的范围.
的范围.点评:本题主要考查两个向量的数量积公式的应用,余弦定理和诱导公式、二倍角公式的应用,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目