Question

已知点P的坐标（x，y）满足：

x-4y+3≤0 3x+5y≤25 x-1≥0.

及A（2，0），则

OA

•

OP

（O为坐标原点）的最大值是

10

_

/

．

Answer 1

分析：确定可行域，利用向量数量积公式，可得目标函数，结合可行域，即可得到结论．

解答：解：可行域，如图所示，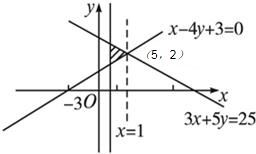
∵P（x，y），A（2，0），
∴

OA

•

OP

=2x，
由

x-4y+3=0 3x+5y=25

，可得

x=5 y=2

∴x的最大值为5，
∴

OA

•

OP

（O为坐标原点）的最大值是10
故答案为：10

点评：本题考查线性规划知识，考查数形结合的数学思想，属于中档题．