题目内容
已知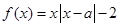 .
.
(1)当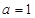 时,解不等式
时,解不等式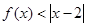 ;
;
(2)当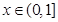 时,
时,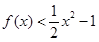 恒成立,求实数
恒成立,求实数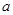 的取值范围.
的取值范围.
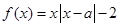 .
.(1)当
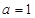 时,解不等式
时,解不等式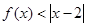 ;
;(2)当
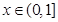 时,
时,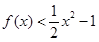 恒成立,求实数
恒成立,求实数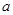 的取值范围.
的取值范围. (1) (2)
(2)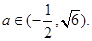
 (2)
(2)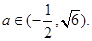
本试题主要是关于绝对值不等式的求解,以及函数的最值问题的运用。
(1)利用去掉绝对值符号,分为三段论来讨论得到解集。
(2)要是不等式恒成立,转换为关于x的函数与参数的不等式关系,借助于最值得到结论。解:(1)当a=1时,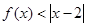 ,即
,即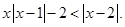 (※)
(※)
① 当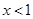 时,由(※)
时,由(※)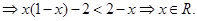
又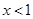 ,
,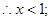 ………………2分
………………2分
②当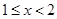 时,由(※)
时,由(※)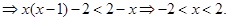
又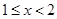 ,
,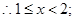 ………………4分
………………4分
③ 当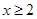 时,由(※)
时,由(※)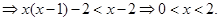
又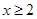 ,
,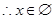 ………………6分
………………6分
综上:由①②③知原不等式的解集为 …………7分
…………7分
(2)当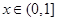 时,
时, ,即
,即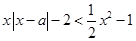 恒成立,
恒成立,
也即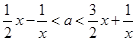 在
在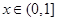 上恒成立。………………10分
上恒成立。………………10分
而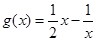 在
在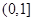 上为增函数,故
上为增函数,故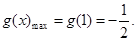
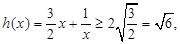
当且仅当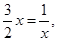 即
即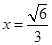 时,等号成立.
时,等号成立.
故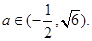 ………………13分
………………13分
(1)利用去掉绝对值符号,分为三段论来讨论得到解集。
(2)要是不等式恒成立,转换为关于x的函数与参数的不等式关系,借助于最值得到结论。解:(1)当a=1时,
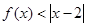 ,即
,即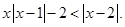 (※)
(※)① 当
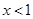 时,由(※)
时,由(※)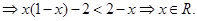
又
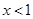 ,
,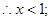 ………………2分
………………2分②当
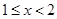 时,由(※)
时,由(※)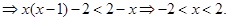
又
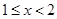 ,
,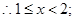 ………………4分
………………4分③ 当
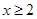 时,由(※)
时,由(※)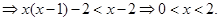
又
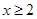 ,
,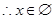 ………………6分
………………6分综上:由①②③知原不等式的解集为
 …………7分
…………7分(2)当
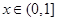 时,
时, ,即
,即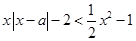 恒成立,
恒成立,也即
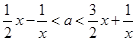 在
在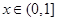 上恒成立。………………10分
上恒成立。………………10分而
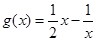 在
在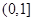 上为增函数,故
上为增函数,故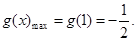
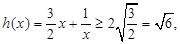
当且仅当
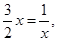 即
即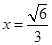 时,等号成立.
时,等号成立.故
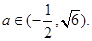 ………………13分
………………13分
练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
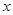 ,不等式
,不等式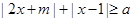 恒成立时,若实数
恒成立时,若实数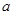 的最大值为3,则实数
的最大值为3,则实数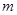 的值为 .
的值为 .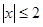 ,
,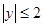 ,点
,点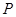 的坐标为
的坐标为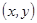
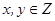 时,求
时,求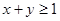 的概率。
的概率。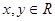 时,求
时,求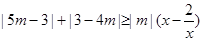 恒成立,则
恒成立,则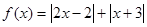
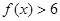 ;
;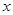 的不等式
的不等式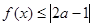 的解集不是空集,求
的解集不是空集,求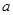 得取值范围.
得取值范围.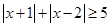
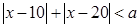 的解集不是空集,则实数a的取值范围为_____________.
的解集不是空集,则实数a的取值范围为_____________.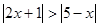 的解集是 .
的解集是 .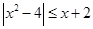 的解集是
的解集是