题目内容
(本小题满分13分)
设命题 :关于x的函数
:关于x的函数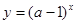 为增函数;命题
为增函数;命题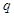 :不等式
:不等式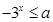 对一切正实数均成立.
对一切正实数均成立.
(1)若命题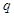 为真命题,求实数
为真命题,求实数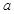 的取值范围;
的取值范围;
(2)命题“ 或
或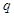 ”为真命题,且“
”为真命题,且“ 且
且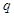 ”为假命题,求实数
”为假命题,求实数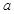 的取值范围.
的取值范围.
设命题
 :关于x的函数
:关于x的函数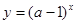 为增函数;命题
为增函数;命题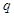 :不等式
:不等式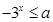 对一切正实数均成立.
对一切正实数均成立. (1)若命题
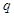 为真命题,求实数
为真命题,求实数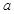 的取值范围;
的取值范围;(2)命题“
 或
或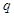 ”为真命题,且“
”为真命题,且“ 且
且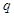 ”为假命题,求实数
”为假命题,求实数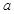 的取值范围.
的取值范围.(1)实数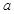 的取值范围是
的取值范围是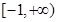 ; (2)实数
; (2)实数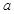 的取值范围是
的取值范围是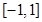 .
.
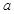 的取值范围是
的取值范围是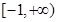 ; (2)实数
; (2)实数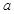 的取值范围是
的取值范围是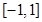 .
.(1)q真,由x>0得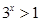 ,所以
,所以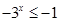 ,所以
,所以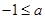 .
.
(2) 由命题“ 或q”为真,且“
或q”为真,且“ 且q”为假,得命题
且q”为假,得命题 、q一真一假,然后按照两种情况求解,再求并集即可.
、q一真一假,然后按照两种情况求解,再求并集即可.
解:(1)当命题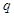 为真命时,由
为真命时,由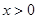 得
得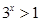 ,∴
,∴ ,
,
不等式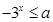 对一切正实数均成立,∴
对一切正实数均成立,∴
∴实数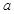 的取值范围是
的取值范围是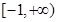 ; ………6分
; ………6分
(2)由命题“ 或q”为真,且“
或q”为真,且“ 且q”为假,得命题
且q”为假,得命题 、q一真一假………8分
、q一真一假………8分
①当 真
真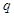 假时,则
假时,则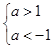 ,无解;………10分
,无解;………10分
②当 假
假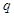 真时,则
真时,则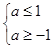 ,得
,得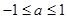 ,………12分
,………12分
∴实数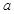 的取值范围是
的取值范围是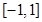 .………13分
.………13分
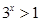 ,所以
,所以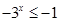 ,所以
,所以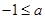 .
.(2) 由命题“
 或q”为真,且“
或q”为真,且“ 且q”为假,得命题
且q”为假,得命题 、q一真一假,然后按照两种情况求解,再求并集即可.
、q一真一假,然后按照两种情况求解,再求并集即可.解:(1)当命题
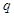 为真命时,由
为真命时,由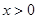 得
得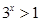 ,∴
,∴ ,
, 不等式
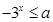 对一切正实数均成立,∴
对一切正实数均成立,∴∴实数
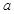 的取值范围是
的取值范围是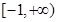 ; ………6分
; ………6分 (2)由命题“
 或q”为真,且“
或q”为真,且“ 且q”为假,得命题
且q”为假,得命题 、q一真一假………8分
、q一真一假………8分 ①当
 真
真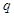 假时,则
假时,则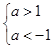 ,无解;………10分
,无解;………10分 ②当
 假
假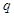 真时,则
真时,则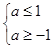 ,得
,得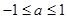 ,………12分
,………12分 ∴实数
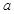 的取值范围是
的取值范围是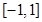 .………13分
.………13分
练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 的必要非充分条件;
的必要非充分条件; 中,A>B是sinA>sinB的充要条件;
中,A>B是sinA>sinB的充要条件; 的充分非必要条件;
的充分非必要条件; 的充要条件.
的充要条件. ,
, ,且
,且 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围. 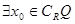 ,
,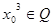 ”的否定是 ( )
”的否定是 ( )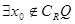 ,
,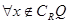 ,
,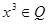
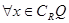 ,
,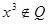
 是定义在
是定义在 上的函数,
上的函数, ,那么“对任意的
,那么“对任意的 ,
, 恒成立”的充要条件是( )
恒成立”的充要条件是( ) 或
或 恒成立
恒成立 或
或 恒成立
恒成立 恒成立
恒成立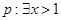 ,
,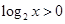 ,则
,则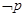 为 .
为 . 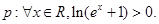 则
则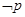 为
为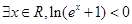
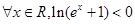
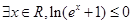
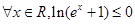
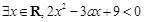 ”为假命题,则实数
”为假命题,则实数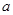 的取值范围是
的取值范围是