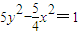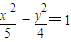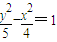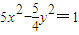题目内容
已知双曲线x2-4y2=4,求过点A(3,-1)且被A平分的弦MN所在的直线方程.
思路解析:设而不求,即设出A、B的坐标,联立方程组,利用韦达定理,整体消参.也可用对称性解决. 解法一:设过A(3,-1)的直线方程为y=k(x-3)-1, 代入双曲线方程,得x2-4[k(x-3)-1]2=4. 整理得(4k2-1)x2-8k(3k+1)x+36k2+24k+8=0. 若直线与双曲线交于M(x1,y1),N(x2,y2)两点,则Δ≥0, 由韦达定理,得x1+x2= ∵A平分MN,∴ ∴MN存在. ∴所求直线方程y=- 解法二:设M(x1,y1),N(x2,y2),则 由(1)-(2),得x12-x22=4(y12-y22),即 将(3)、(4)代入上式,得kMN= 故MN所在直线方程为y+1=- 即3x+4y-5=0,与双曲线方程x2-4y=4联立,消去y得5x2-30x+41=0. ∵Δ=302-820>0,∴M、N两点存在. 所求直线方程为3x+4y-5=0. 解法三:设弦MN一个端点的坐标为(x,y),则弦另一个端点的坐标为(6-x,-2-y). 若MN存在,则M、N两点在双曲线上, ∴x2-4y2=4, ① 且(6-x)2-4(-2-y)2=4. ② ①-②整理,得3x+4y-5=0. 与双曲线方程x2-4y2=4联立,消去y,得5x2-30x+41=0, ∵Δ=302-820>0,∴该直线与双曲线相交于两点. ∴所求直线方程为3x+4y-5=0. 误区警示 直线与双曲线的关系中,都需要对所求直线的存在性进行验证(这一点与椭圆不同),否则就容易出现错误.![]() . ①
. ①![]() =3,解得k=-
=3,解得k=-![]() ,代入①验证,满足Δ≥0,
,代入①验证,满足Δ≥0,![]() (x-3)-1,即3x+4y-5=0.
(x-3)-1,即3x+4y-5=0.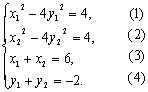
![]() =
=![]() .
.![]() =-
=-![]() ,
,![]() (x-3),
(x-3),


天下中考系列答案
听力总动员系列答案
听力一本通系列答案
通城学典计算能手系列答案
同步奥数培优系列答案
同步测试天天向上系列答案
同步课时精练系列答案
创新作业同步练习系列答案
同步练习浙江教育出版社系列答案
| y2 |
| a2 |
| x2 |
| b2 |
A、5y2-
| ||||
B、
| ||||
C、
| ||||
D、5x2-
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
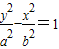 的一个焦点与抛物线x2=4y的焦点重合,且双曲线的实轴长是虚轴长的一半,则该双曲线的方程为( )
的一个焦点与抛物线x2=4y的焦点重合,且双曲线的实轴长是虚轴长的一半,则该双曲线的方程为( )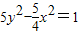
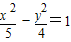
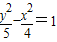
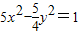
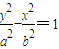 的一个焦点与抛物线x2=4y的焦点重合,且双曲线的实轴长是虚轴长的一半,则该双曲线的方程为( )
的一个焦点与抛物线x2=4y的焦点重合,且双曲线的实轴长是虚轴长的一半,则该双曲线的方程为( )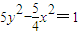
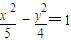
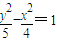
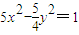
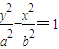 的一个焦点与抛物线x2=4y的焦点重合,且双曲线的实轴长是虚轴长的一半,则该双曲线的方程为( )
的一个焦点与抛物线x2=4y的焦点重合,且双曲线的实轴长是虚轴长的一半,则该双曲线的方程为( )