题目内容
【题目】已知直线l的方程为y=![]() x-2
x-2![]() ,又直线l过椭圆C:
,又直线l过椭圆C:![]() (a>b>0)的右焦点,且椭圆的离心率为
(a>b>0)的右焦点,且椭圆的离心率为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点D(0,1)的直线与椭圆C交于点A,B,求△AOB的面积的最大值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
试题(Ⅰ)通过分析可知直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,得
,得![]() ,又
,又![]() ,得
,得![]() ,利用
,利用![]() ,可得
,可得![]() 即可求得椭圆方程为
即可求得椭圆方程为![]() ;(Ⅱ)可设直线
;(Ⅱ)可设直线![]() 方程为
方程为![]() ,
,
设![]() ,故
,故![]() ,为此可联立
,为此可联立 ,整理得
,整理得![]() ,利用韦达定理,求出
,利用韦达定理,求出![]() ,
,
可得![]()
 ,
,
令![]() 则
则![]()
![]() ,[科当
,[科当![]() ,即
,即![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.
试题解析:(Ⅰ)∵![]() ,∴椭圆的焦点为直线
,∴椭圆的焦点为直线![]() 与
与![]() 轴的交点,
轴的交点,
∵直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,∴椭圆的焦点为
,∴椭圆的焦点为![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,∴
,∴![]()
∴椭圆方程为![]() .
.
(Ⅱ) 直线![]() 的斜率显然存在,设直线
的斜率显然存在,设直线![]() 方程为
方程为![]()
设![]() ,由
,由 ,得
,得![]() ,
,
显然![]() ,
,![]()
![]()


令![]() 则
则![]() ,
,![]() ,
,
![]() ,即
,即![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
相关题目
【题目】高三年级有500名学生,为了了解数学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组 | 频数 | 频率 |
| ① | ② |
| 0.050 | |
| 0.200 | |
| 12 | 0.300 |
| 0.275 | |
| 0.050 | |
合计 | ④ |
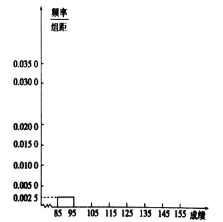
(1)根据上面图表,①②④处的数值分别为______,______,______;
(2)在所给的坐标系中画出![]() 的频率分布直方图;
的频率分布直方图;
(3)根据题中信息估计总体平均数,并估计总体落在![]() 中的概率.
中的概率.