题目内容
7.若函数f(x)=-2x3+2tx2+1存在唯一的零点,则实数t的取值范围为t>-$\frac{3}{2}$.分析 求解导数f′(x)=-6x2+4tx,分类讨论得出极值点,
根据单调性判断极值的大小,即可得出零点的个数.
解答 解:∵函数f(x)=-2x3+2tx2+1,
∴f′(x)=-6x2+4tx=0,
∴x=0,x=$\frac{2t}{3}$
(1)当t=0时,f(x=-2x3+1单调递减,
f(0)=1>0,f(2)=-15<0
∴存在唯一的零点,是正数.
(2)当t>0时,
f′(x)=-6x2+4tx>0,即0$<x<\frac{2t}{3}$
f′(x)=-6x2+4tx<0,即x<0,x$>\frac{2t}{3}$
∴f(x)在(-∞,0),($\frac{2t}{3}$,+∞)单调递减
在(0,$\frac{2t}{3}$)单调递增
∴极大值f($\frac{2t}{3}$)>f(1),极小值f(0)=1>0,
∴存在唯一的零点,
(3)当t<0时,
f′(x)=-6x2+4tx>0,即$\frac{2t}{3}$<x<0
f′(x)=-6x2+4tx<0,即x<$\frac{2t}{3}$,x>0
∴f(x)在(-∞,$\frac{2t}{3}$),(0,+∞)单调递减
在($\frac{2t}{3}$,0)单调递增
∴极小值f($\frac{2t}{3}$)<f(1),极大值f(0)=1>0,
∵只需极小值f($\frac{2t}{3}$)>0即可,
$\frac{8{t}^{3}}{27}$+1>0,且t<0
∴-$\frac{3}{2}$<t<0,
综上:-$\frac{3}{2}$<t<0,或t≥0
故答案为:t>-$\frac{3}{2}$.
点评 本题考查了利用导数研究函数的单调性极值与最值、函数的零点,考查了分类讨论方法、推理能力与计算能力,属于中档题.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
18.如图为某几何体的三视图,则该几何体的体积等于( )
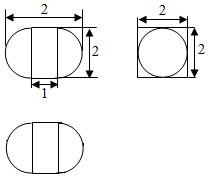

| A. | $4+\frac{2π}{3}$ | B. | $8+\frac{2π}{3}$ | C. | $4+\frac{4π}{3}$ | D. | $6+\frac{4π}{3}$ |
15.在复平面内,复数$\frac{1-2i}{2+i}$对应的点的坐标为( )
| A. | ($\frac{4}{5}$,$\frac{3}{5}$) | B. | ($\frac{4}{5}$,-$\frac{3}{5}$) | C. | (0,1) | D. | (0,-1) |
12.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为( )
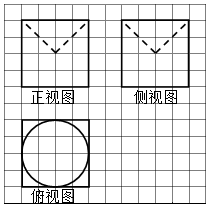

| A. | 96 | B. | $80+4\sqrt{2}π$ | C. | $96+4(\sqrt{2}-1)π$ | D. | $96+4(2\sqrt{2}-1)π$ |
17.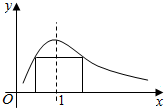 一矩形的一边在x轴上,另两个顶点在函数y=$\frac{2x}{1+{x}^{2}}$(x>0)的图象上,如图,则此矩形绕x轴旋转而成的几何体的体积的最大值是( )
一矩形的一边在x轴上,另两个顶点在函数y=$\frac{2x}{1+{x}^{2}}$(x>0)的图象上,如图,则此矩形绕x轴旋转而成的几何体的体积的最大值是( )
 一矩形的一边在x轴上,另两个顶点在函数y=$\frac{2x}{1+{x}^{2}}$(x>0)的图象上,如图,则此矩形绕x轴旋转而成的几何体的体积的最大值是( )
一矩形的一边在x轴上,另两个顶点在函数y=$\frac{2x}{1+{x}^{2}}$(x>0)的图象上,如图,则此矩形绕x轴旋转而成的几何体的体积的最大值是( )| A. | π | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
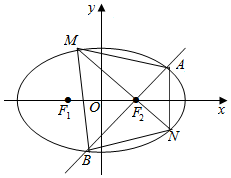 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,直线l经过F2且交椭圆C于A,B两点(如图),△ABF1的周长为4$\sqrt{2}$,原点O到直线l的最大距离为1.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,直线l经过F2且交椭圆C于A,B两点(如图),△ABF1的周长为4$\sqrt{2}$,原点O到直线l的最大距离为1.