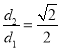题目内容
【题目】已知向量![]() 函数
函数![]()
(1)![]() 求函数
求函数![]() 的值域;
的值域;
(2)求方程![]() ,在
,在![]() 内的所有实数根之和.
内的所有实数根之和.
【答案】(1) ![]() ;(2) 0<k<
;(2) 0<k<![]() ,所有实数根之和
,所有实数根之和![]() , k=0时,
, k=0时, ![]() .
.
【解析】试题分析:(1)运用向量的数量积的坐标表示和二倍角的余弦公式及两角和的正弦公式,结合正弦函数的图象和性质,即可得到所求函数的值域;
(2)由题意可得![]() ,讨论当0<k<
,讨论当0<k<![]() 时,当k=0时,结合函数的对称性和周期性,即可得到所求所求实根之和.
时,当k=0时,结合函数的对称性和周期性,即可得到所求所求实根之和.
试题解析:
(1)解:f(x)=ab﹣1=1×2cos2x+ sin2x-1
=1+cos2x+ sin2x﹣1=![]() sin(2x+
sin(2x+ ![]() )
) ![]()
∴f(x) ![]()
(2)解:由方程f(x)=k,(0![]() k<
k<![]() ),得
),得 ![]() .
.
∵ sin(2x+ ![]() )的周期T=π,又 ∵ sin(2x+
)的周期T=π,又 ∵ sin(2x+ ![]() )在
)在 ![]() 内有2个周期.
内有2个周期.
0<k<![]() ∵
∵ ![]() ,∴方程
,∴方程![]() 在
在 ![]() 内有4个交点,即有4个 实根.根据图象的对称性,有
内有4个交点,即有4个 实根.根据图象的对称性,有 ![]() ,
,
∴所有实数根之和![]()
k=0时, ![]() .
.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目