题目内容
若函数 在区间
在区间 上是增函数,则有( )
上是增函数,则有( )
A. | B. | C. | D. |
C
解析试题分析: ,如果
,如果 ,则
,则 在
在 上单调递减,在
上单调递减,在 上也单调递减;如果
上也单调递减;如果 ,则
,则 在
在 上单调递增,在
上单调递增,在 上也单调递增。因为
上也单调递增。因为 在区间
在区间 上是增函数,所以
上是增函数,所以 ,且
,且 为
为 的一个子区间,所以
的一个子区间,所以 ,所以
,所以 .
.
考点:本题主要考查已知函数的单调区间求参数的取值范围.
点评:对于这类问题,学生应该首先分析已知函数的单调性,如此题 应该先化为
应该先化为 ,借助于函数
,借助于函数 的单调性求出要考查函数的单调性,然后在解题过程中还要注意已知区间与要求区间之间的关系,更要注意端点出的值能不能取到.
的单调性求出要考查函数的单调性,然后在解题过程中还要注意已知区间与要求区间之间的关系,更要注意端点出的值能不能取到.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
已知函数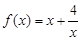 ,且当
,且当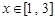 ,
,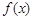 的值域是
的值域是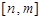 ,则
,则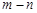 的值是
的值是
A.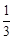 | B.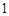 | C. | D.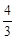 |
设集合 ,
, 则
则 ( )
( )
A. | B. | C. | D. |
设函数 ,则
,则 ( )
( )
A.在区间 内均有零点 内均有零点 |
B.在区间 内均无零点 内均无零点 |
C.在区间 内有零点,在区间 内有零点,在区间 内无零点 内无零点 |
D.在区间 内无零点,在区间 内无零点,在区间 内有零点 内有零点 |
如果两个函数的对应关系相同,值域相同,但定义域不同,则这两个函数为“同族函数”,那么函数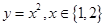 的“同族函数”有( )
的“同族函数”有( )
| A.3个 | B.7个 | C.8个 | D.9个 |
下列各组函数中表示同一函数的是 ( )
① 与
与 ;②
;② 与
与 ;
;
③ 与
与 ;④
;④ 与
与 .
.
| A.①② | B.②③ | C.③④ | D.①④ |
函数 的值域是
的值域是
A. | B. | C. | D. |
已知偶函数 在区间
在区间 上单调递增,则满足不等式
上单调递增,则满足不等式 的
的 的取值范围是 ( )
的取值范围是 ( )
A.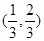 | B. | C.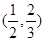 | D. |
函数
 在区间
在区间 上有最大值10,则函数
上有最大值10,则函数 在区间
在区间 上有( )
上有( )
| A.最大值-10 | B.最小值-10 | C.最小值—26 | D.最大值-26 |