题目内容
已知函数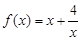 ,且当
,且当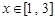 ,
,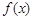 的值域是
的值域是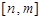 ,则
,则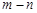 的值是
的值是
A.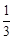 | B.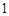 | C. | D.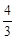 |
B
解析试题分析:根据题意可知函数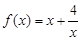 是对勾函数,且当x>2时,函数单调递增,在[1,2]时单调递减,故
是对勾函数,且当x>2时,函数单调递增,在[1,2]时单调递减,故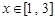 ,
,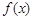 的最小值为f(2)=4,最大值为f(4)=f(1)=5,则由
的最小值为f(2)=4,最大值为f(4)=f(1)=5,则由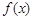 的值域是
的值域是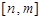 ,那么可知在m=5,n=4,故m-n=1.选B.
,那么可知在m=5,n=4,故m-n=1.选B.
考点:本试题主要考查了函数单调性的判定以及函数单调性性质的运用。
点评:解决该试题的关键是理解函数的单调性,运用定义法来证明即可,或者利用对勾函数的性质,直接判定单调性,进而得到最值。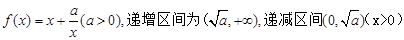 这是重要的结论。
这是重要的结论。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果二次函数y=x2+mx+(m+3)有两个不同的零点,则m的取值范围是
| A.(-2,6) | B.[-2,6] |
| C.{-2,6} | D.(-∞,-2)∪(6,+∞) |
下列函数中,与函数 有相同定义域的是( )
有相同定义域的是( )
A. | B.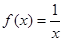  | C.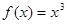 | D. |
函数f(x)= 的零点所在的区间是( )
的零点所在的区间是( )
A.(0, ) ) | B.( ,1) ,1) | C.(1, ) ) | D.( ,2) ,2) |
下列函数中是偶函数的是
A.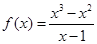 | B.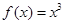 | C.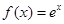 | D.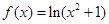 |
已知函数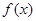 是R上的单调增函数且为奇函数,数列
是R上的单调增函数且为奇函数,数列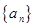 是等差数列,
是等差数列,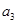 >0,则
>0,则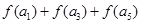 的值 ( )
的值 ( )
| A.恒为正数 | B.恒为负数 |
| C.恒为0 | D.可以为正数也可以为负数 |
函数 ,则
,则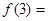
| A.1 | B.2 | C.3 | D.4 |
设函数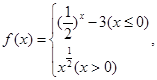 已知
已知 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
若函数 在区间
在区间 上是增函数,则有( )
上是增函数,则有( )
A. | B. | C. | D. |