题目内容
设函数 ,则
,则 ( )
( )
A.在区间 内均有零点 内均有零点 |
B.在区间 内均无零点 内均无零点 |
C.在区间 内有零点,在区间 内有零点,在区间 内无零点 内无零点 |
D.在区间 内无零点,在区间 内无零点,在区间 内有零点 内有零点 |
A
解析试题分析:根据所给的四个命题中所提到两个区间的端点对应的数字,做出三个数字对应的函数值,观察两个端点的函数值的符号是否相反,根据零点的判定定理得到结果.
因为f( )=-
)=- -1<0,f(1)=
-1<0,f(1)= >0, f(e)=
>0, f(e)= -1<0所以根据零点存在性定理可知f(
-1<0所以根据零点存在性定理可知f( )f(1)<0,f(1)f(e)<0,因此可知选A
)f(1)<0,f(1)f(e)<0,因此可知选A
考点:本试题主要考查了查函数零点,本题是一个基础题.
点评:本题解题的关键是看出函数在几个点对应的函数值的符号.

练习册系列答案
相关题目
函数f(x)= 的零点所在的区间是( )
的零点所在的区间是( )
A.(0, ) ) | B.( ,1) ,1) | C.(1, ) ) | D.( ,2) ,2) |
设函数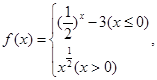 已知
已知 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
函数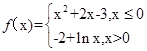 的零点个数为 ( )
的零点个数为 ( )
| A.0 | B.1 | C.2 | D.3 |
设函数 ,则
,则 的表达式是( )
的表达式是( )
A. | B. | C. | D. |
若函数 在区间
在区间 上是增函数,则有( )
上是增函数,则有( )
A. | B. | C. | D. |
已知函数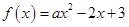 在
在 上是减函数,则
上是减函数,则 的取值范围是( )
的取值范围是( )
A. | B. | C. 或 或 | D. |
函数 是R上的偶函数,且在
是R上的偶函数,且在 上单调递增,则下列各式成立的是
上单调递增,则下列各式成立的是
A. | B. |
C. | D. |
