题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)令![]() ,若曲线
,若曲线![]() 在点
在点![]() 处的切线的纵截距为
处的切线的纵截距为![]() ,求
,求![]() 的值;
的值;
(2)设![]() ,若方程
,若方程![]() 在区间
在区间![]() 内有且只有两个不相等的实数根,求实数
内有且只有两个不相等的实数根,求实数![]() 的取值范围.
的取值范围.
【答案】(1)6;(2)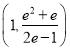
【解析】
(1)求得![]() 在点
在点![]() 处的切线方程,根据切线的截距为
处的切线方程,根据切线的截距为![]() 列方程,解方程求得
列方程,解方程求得![]() 的值.
的值.
(2)将方程![]() 转化为
转化为![]() ,构造函数
,构造函数![]() ,利用
,利用![]() 研究函数
研究函数![]() 在
在![]() 内的零点,结合零点存在性定理列不等式组,解不等式组求得
内的零点,结合零点存在性定理列不等式组,解不等式组求得![]() 的取值范围.
的取值范围.
(1)由题设知,
![]() ,
,![]() ,
,
则![]() ;
;
∴![]() ,又
,又![]() ,
,
∴切点为![]() ,
,
则切线方程为![]() ,
,
令![]() ,则
,则![]() ,
,
由题设知,![]() ,
,
∴![]() ;
;
(2)∵![]() ,∴
,∴![]() ,
,
则方程![]() ,
,
即为![]() ,
,
即为![]() ;
;
令![]() ,于是原方程在区间
,于是原方程在区间![]() 内根的问题,
内根的问题,
转化为函数![]() 在
在![]() 内的零点问题;
内的零点问题;
∵![]()
![]() ;
;
∵![]() ,∴当
,∴当![]() 时,
时,
![]() ,
,![]() 是减函数,
是减函数,
当![]() 时,
时,![]() ,
,![]() 是增函数,
是增函数,
若使![]() 在
在![]() 内有且只有两个不相等的零点,
内有且只有两个不相等的零点,
只需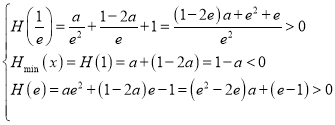 即可,
即可,
解得,![]() ,
,
即![]() 的取值范围是
的取值范围是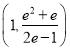 .
.

练习册系列答案
相关题目