题目内容
已知函数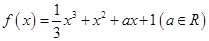 .
.
(1)求函数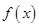 的单调区间;
的单调区间;
(2)当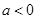 时,试讨论是否存在
时,试讨论是否存在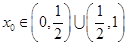 ,使得
,使得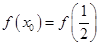 .
.
(1)详见解析;(2)详见解析.
解析试题分析:(1)先求出导数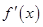 为二次函数,对
为二次函数,对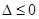 和
和 进行分类讨论,根据导数的正负求出函数
进行分类讨论,根据导数的正负求出函数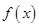 的单调区间;(2)由作差法
的单调区间;(2)由作差法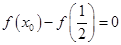 将等式进行因式分解,得到
将等式进行因式分解,得到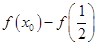
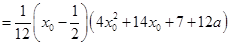 ,于是将问题转化为方程
,于是将问题转化为方程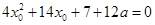 在
在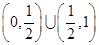 上有解,并求出该方程的两根,并判定其中一根
上有解,并求出该方程的两根,并判定其中一根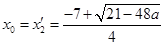 在区间
在区间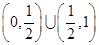 上,并由
上,并由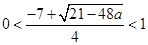 以及
以及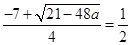 确定满足条件
确定满足条件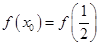 时
时 的取值范围,然后取相应的补集作为满足条件
的取值范围,然后取相应的补集作为满足条件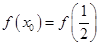 时
时 的取值范围.
的取值范围.
(1)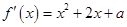 ,方程
,方程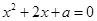 的判别式为
的判别式为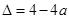 ,
,
①当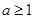 时,
时,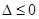 ,则
,则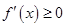 ,此时
,此时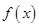 在
在 上是增函数;
上是增函数;
②当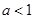 时,方程
时,方程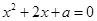 的两根分别为
的两根分别为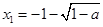 ,
,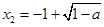 ,
,
解不等式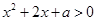 ,解得
,解得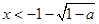 或
或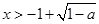 ,
,
解不等式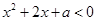 ,解得
,解得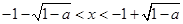 ,
,
此时,函数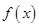 的单调递增区间为
的单调递增区间为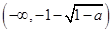 和
和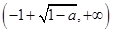 ,
,
单调递减区间为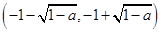 ;
;
综上所述,当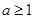 时,函数
时,函数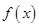 的单调递增区间为
的单调递增区间为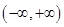 ,
,
当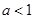 时,函数
时,函数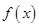 的单调递增区间为
的单调递增区间为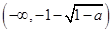 和
和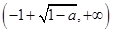 ,
,
单调递减区间为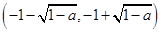 ;
;
(2)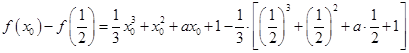

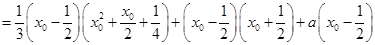
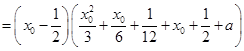
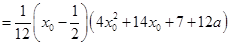 ,
,
若存在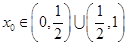 ,使得
,使得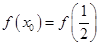 ,
,
必须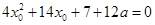 在
在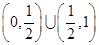 上有解,
上有解,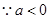 ,
,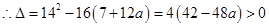 ,
,
方程的两根为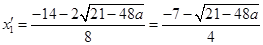 ,
,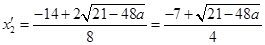 ,
,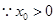 ,
,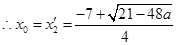 ,
,
依题意,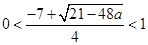 ,即
,即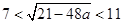 ,
,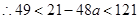 ,即
,即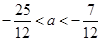 ,
,
又由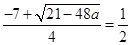 得
得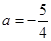 ,
,
故欲使

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
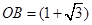 百米,边界线AC始终过点B,边界线OA、OC满足∠AOC=75°,∠AOB=30°,∠BOC=45°,设
百米,边界线AC始终过点B,边界线OA、OC满足∠AOC=75°,∠AOB=30°,∠BOC=45°,设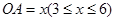 百米,
百米, 百米.
百米.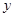 表示成
表示成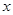 的函数,并求出函数
的函数,并求出函数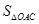 最小,并求出其面积的最小值.
最小,并求出其面积的最小值.
 有最小正周期2,且当
有最小正周期2,且当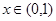 时,
时, .
.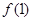 和
和 的值;
的值;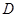 的函数
的函数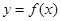 ,若同时满足:
,若同时满足: 在
在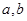 ]
]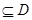 ,使
,使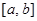 上的值域为
上的值域为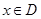 )叫做闭函数.
)叫做闭函数.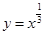 符合条件②的区间
符合条件②的区间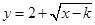 是闭函数,求实数
是闭函数,求实数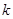 的取值范围.
的取值范围. 及二次函数
及二次函数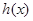 满足:
满足: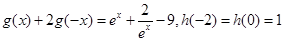 且
且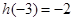 .
.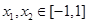 ,均有
,均有 成立,求
成立,求 的取值范围;
的取值范围; ,讨论方程
,讨论方程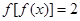 的解的个数情况.
的解的个数情况.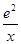 (x>0).
(x>0). 在(0,1]上解的个数.
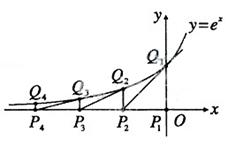
在(0,1]上解的个数. 轴的垂线交曲线
轴的垂线交曲线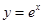 于点
于点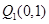 ,曲线在
,曲线在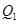 点处的切线与
点处的切线与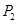 .再从
.再从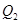 ,依次重复上述过程得到一系列点:
,依次重复上述过程得到一系列点: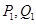 ;
;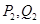 ;…;
;…; ,记
,记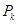 点的坐标为
点的坐标为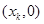 (
(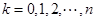 ).
).
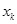 与
与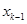 的关系(
的关系(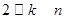 );
);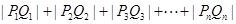 .
. 且满足
且满足 ,则
,则 的最小值为 ;若
的最小值为 ;若 又满足
又满足 的取值范围是 .
的取值范围是 .