题目内容
如图所示,O为△ABC的外心,以线段OA、OB为邻边作平行四边形,第四个顶点为D,再以OC、OD为邻边作平行四边形,它的第四个顶点为H.

(1)若![]() =a,
=a, ![]() =b,
=b, ![]() =c.
=c.![]() =h,试用a、b、c表示h;
=h,试用a、b、c表示h;
(2)证明:![]() ⊥
⊥![]() ;
;
(3)若△ABC中的∠A=60°,∠B=45°,外接圆的半径为R,用R表示|h|.

解:(1)由题意知![]() +
+![]() =
=![]() ,
,![]() ?=
?=![]() +
+![]() ,故
,故![]() =
=![]() +
+![]() +
+![]() ,即h=a+b+c.
,即h=a+b+c.
(2)![]() =
=![]() -
-![]() =a+b+c-a=b+c,?
=a+b+c-a=b+c,?![]() =
=![]() -
-![]() =c-b.?则
=c-b.?则![]() ·
·![]() =(b+c)(c-b)=c2-b2.?又|
=(b+c)(c-b)=c2-b2.?又|![]() |=|
|=|![]() |=|
|=|![]() |,故|c|=|b|,即c2=b2.?∴
|,故|c|=|b|,即c2=b2.?∴![]() ·
·![]() =0,即?AH⊥BC.?
=0,即?AH⊥BC.?
(3)∠A=60°,∠BOC=2∠A=120°,故在△BOC中,由余弦定理有?|![]() |2=|
|2=|![]() |2+|
|2+|![]() |2-2|
|2-2|![]() |·|
|·|![]() |·cos120°=3R2,即|
|·cos120°=3R2,即|![]() |=
|=![]() R.?同理|
R.?同理|![]() |=
|=![]() R,且∠AOC=2∠B=90°,则∠AOB=2∠C=150°.?∴a·c=|a||b|·cos150°=-
R,且∠AOC=2∠B=90°,则∠AOB=2∠C=150°.?∴a·c=|a||b|·cos150°=-![]() R2.?又∵∠AOC=90°,?∴a·c=0,b·c=|b|·|c|·cos120°=-
R2.?又∵∠AOC=90°,?∴a·c=0,b·c=|b|·|c|·cos120°=-![]() R2.?∴|h|=
R2.?∴|h|=![]() =
=![]() =
=![]() =
=![]() .?∴|h|=
.?∴|h|=![]() R,即|h|为
R,即|h|为![]() R.
R.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)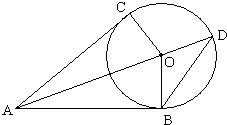 (2011•广东模拟)(几何证明选讲)如图所示,AC和AB分别是圆O的切线,B、C 为切点,且OC=3,AB=4,延长OA到D点,则△ABD的面积是
(2011•广东模拟)(几何证明选讲)如图所示,AC和AB分别是圆O的切线,B、C 为切点,且OC=3,AB=4,延长OA到D点,则△ABD的面积是 A:如图所示,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于点D,BC=4cm,
A:如图所示,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于点D,BC=4cm, (2013•潮州二模)如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=
(2013•潮州二模)如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD= 选修4-1:几何证明选讲
选修4-1:几何证明选讲