题目内容

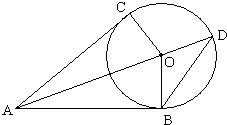（2011•广东模拟）（几何证明选讲）如图所示，AC和AB分别是圆O的切线，B、C 为切点，且OC=3，AB=4，延长OA到D点，则△ABD的面积是
48
5
48
5
．
分析：利用勾股定理求出AO，可得AD的值，由直角三角形相似得 
OB
h
=
AO
AD
，求出h 值，代入△ABD的面积公式进行运算．
解答：解：由题意得 AO=
AB2+OB2
=
16+9
=5，AD=5+3=8，设D到AB的距离等于h，
由直角三角形相似得 
OB
h
=
AO
AD
，
3
h
=
5
8
，h=
24
5
．
故△ABD的面积等于 
1
2
AB•h=
48
5
，
故答案为：
48
5
．
点评：本题考查直线和圆相切的性质，相似三角形的性质，求出D到AB的距离等于h是解题的关键．
练习册系列答案
相关题目
（2011•广东模拟）给定函数f(x)=
x2
2(x-1)

（1）试求函数f（x）的单调减区间；
（2）已知各项均为负的数列{an}满足，4Sn•f(
1
an
)=1，求证：-
1
an+1
＜ln
n+1
n
＜-
1
an
；
（3）设bn=-
1
an
，Tn为数列 {bn} 的前n项和，求证：T2012-1＜ln2012＜T2011．
（2011•广东模拟）已知集合M={y|y=x2-1，x∈R}，N={x|y=
2-x2
}，则M∩N=（　　）
（2011•广东模拟）已知函数f（x）=
a-x
+
x
（a∈N*），对定义域内任意x1，x2，满足|f（x1）-f（x2）|＜1，则正整数a的取值个数是
5
5
．
（2011•广东模拟）已知命题“?x∈R，x2+2ax+1＜0”是真命题，则实数a的取值范围是（　　）
（2011•广东模拟）已知线段AB的两个端点分别为A（0，1），B（1，0），P（x，y）为线段AB上不与端点重合的一个动点，则(x+
1
x
)(y+
1
y
)的最小值为
25
4
25
4
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网