题目内容
设抛物线y2=4x的焦点为F,过点M(-1,0)的直线在第一象限交抛物线于A、B,使 ,则直线AB的斜率k=
,则直线AB的斜率k=
- A.

- B.

- C.

- D.

B
分析:由题意可得直线AB的方程 y-0=k (x+1),k>0,代入抛物线y2=4x化简求得x1+x2 和x1•x2,进而得到y1+y2和y1•y2,由 ,解方程求得k的值.
,解方程求得k的值.
解答:抛物线y2=4x的焦点F(1,0),直线AB的方程 y-0=k (x+1),k>0.
代入抛物线y2=4x化简可得 k2x2+(2k2-4)x+k2=0,
∴x1+x2= ,x1•x2=1.
,x1•x2=1.
∴y1+y2= +2k=
+2k= ,
,
y1•y2=k2(x1+x2+x1•x2+1)=4.
又 =(x1-1,y1)•(x2-1,y2)=x1•x2-(x1+x2)+1+y1•y2=8-
=(x1-1,y1)•(x2-1,y2)=x1•x2-(x1+x2)+1+y1•y2=8-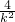 ,
,
∴k= ,
,
故选B.
点评:本题考查直线和圆锥曲线的位置关系,两个向量的数量积公式的应用,得到 8-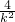 =0,是解题的难点和关键.
=0,是解题的难点和关键.
分析:由题意可得直线AB的方程 y-0=k (x+1),k>0,代入抛物线y2=4x化简求得x1+x2 和x1•x2,进而得到y1+y2和y1•y2,由
 ,解方程求得k的值.
,解方程求得k的值.解答:抛物线y2=4x的焦点F(1,0),直线AB的方程 y-0=k (x+1),k>0.
代入抛物线y2=4x化简可得 k2x2+(2k2-4)x+k2=0,
∴x1+x2=
 ,x1•x2=1.
,x1•x2=1.∴y1+y2=
 +2k=
+2k= ,
,y1•y2=k2(x1+x2+x1•x2+1)=4.
又
 =(x1-1,y1)•(x2-1,y2)=x1•x2-(x1+x2)+1+y1•y2=8-
=(x1-1,y1)•(x2-1,y2)=x1•x2-(x1+x2)+1+y1•y2=8-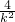 ,
,∴k=
 ,
,故选B.
点评:本题考查直线和圆锥曲线的位置关系,两个向量的数量积公式的应用,得到 8-
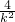 =0,是解题的难点和关键.
=0,是解题的难点和关键. 
练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目