题目内容
求经过直线l1:3x+2y-1=0和l2:5x+2y+1=0的交点,且垂直于直线l3:3x-5y+6=0的直线l的方程.
解 法一 先解方程组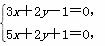
得l1,l2的交点坐标为(-1,2),
再由l3的斜率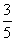 求出l的斜率为-
求出l的斜率为-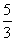 ,
,
于是由直线的点斜式方程求出l:
y-2=-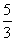 (x+1),即5x+3y-1=0.
(x+1),即5x+3y-1=0.
法二 由于l⊥l3,故l是直线系5x+3y+C=0中的一条,而l过l1,l2的交点(-1,2),
故5×(-1)+3×2+C=0,由此求出C=-1,
故l的方程为5x+3y-1=0.
法三 由于l过l1,l2的交点,故l是直线系3x+2y-1+λ(5x+2y+1)=0中的一条,
将其整理,得(3+5λ)x+(2+2λ)y+(-1+λ)=0.
其斜率-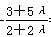 =-
=-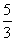 ,解得λ=
,解得λ=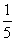 ,
,
代入直线系方程即得l的方程为5x+3y-1=0.

练习册系列答案
相关题目
 是坐标原点,点
是坐标原点,点 ,若点
,若点 为平面区域
为平面区域 上的一个动点,
上的一个动点, 最大值为:
最大值为:



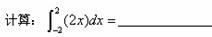
 (x-1)与圆O:x2+y2=1在第一象限内交于点M,且l与y轴交于点A,则△MOA的面积等于________.
(x-1)与圆O:x2+y2=1在第一象限内交于点M,且l与y轴交于点A,则△MOA的面积等于________.