题目内容
【题目】已知双曲线
的左、右两个顶点分别是A1,A2,左、右两个焦点分别是F1,F2,P是双曲线上异于A1,A2的任意一点，给出下列命题，其中是真命题的有（ ）
A.
B.直线
的斜率之积等于定值
C.使得
为等腰三角形的点
有且仅有8个
D.的面积为
【答案】BC
【解析】
结合双曲线的几何性质和常见二级结论推导即可得解.
在
中，两边之差小于第三边，即
，所以A不是真命题；
设点
，有
，
，
直线
的斜率之积
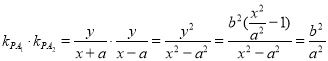，所以B是真命题；
根据双曲线对称性要使
为等腰三角形，则
必为腰，在第一象限双曲线上有且仅有一个点
使
，此时为等腰三角形，
也且仅有一个点
使
，此时
为等腰三角形，同理可得第二三四象限每个象限也有且仅有两个点，一共八个，
所以C是真命题；
，根据焦点三角形面积的二级结论
，所以D不是真命题.
故选：BC
练习册系列答案
相关题目
