Question

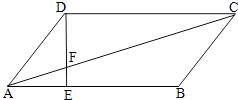
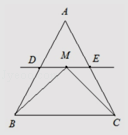
【题目】在△ABC中，D、E分别是AB、AC的中点，M是直线DE上的动点．若△ABC的面积为2，则 + 2的最小值为 ．

Answer 1

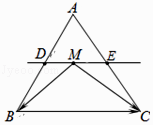
【答案】2
【解析】解：∵D、E是AB、AC的中点， ∴M到BC的距离等于点A到BC的距离的一半，
∴S△ABC=2S△MBC ， 而△ABC的面积2，则△MBC的面积S△MBC=1，
S△MBC= 丨MB丨丨MC丨sin∠BMC=1，
∴丨MB丨丨MC丨= ．
∴ =丨MB丨丨MC丨cos∠BMC= ．
由余弦定理，丨BC丨2=丨BM丨2+丨CM丨2﹣2丨BM丨丨CM丨cos∠BMC，
显然，BM、CM都是正数，
∴丨BM丨2+丨CM丨2≥2丨BM丨丨CM丨，
∴丨BC丨2=丨BM丨2+丨CM丨2﹣2丨BM丨×丨CM丨cos∠BMC
=2× ﹣2× ．
∴ + 2≥ +2× ﹣2×
=2 ，
方法一：令y= ，则y′= ，
令y′=0，则cos∠BMC= ，此时函数在（0， ）上单调减，在（ ，1）上单调增，
∴cos∠BMC= 时， 取得最小值为 ，
+ 2的最小值为2 ；
方法二：令y= ，
则ysin∠BMC+cos∠BMC=2，则 sin（∠BMC+α）=2，
tanα= ，
则sin（∠BMC+α）= ≤1，
解得：y≥ ，
则 + 2的最小值为2 ；
所以答案是：2 ．