题目内容

20．一个正方体的平面展开图及该正方体的直观图的示意图如图所示．
（1）判断平面BEG与平面ACH的位置关系．并证明你的结论；
（2）若正方体棱长为1，求三棱锥F-BEG的体积．

分析 （1）说明EG∥AC且AH∥BG，利用平面与平面平行的判定定理证明平面ACH∥平面BEG．
（2）通过VF-BEG=VE-FBG，直接求解几何体的体积即可．

解答 证：（1）由题F、G、H位置如图，正方体中，EG∥AC且AH∥BG
又AH∩AC=A，EG∩BG=G且
AH、AC∈平面ACH，EG、BG?平面BEG
∴平面ACH∥平面BEG
（2）∵正方体中，EF⊥FG⊥FB
∴VF-BEG=VE-FBG=$\frac{1}{3}$×S△BGF×EF=$\frac{1}{3}$×$\frac{1}{2}$×1×1×1=$\frac{1}{6}$．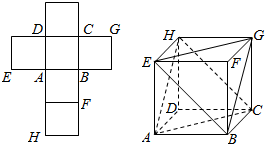

点评 本题考查平面与平面平行的判定定理的应用，几何体的体积的求法，考查计算能力以及空间想象能力．

练习册系列答案
相关题目
10．在△ABC中，BD：DC=2：1，AE：EC=1：3，求OB：OE．
11．设向量$\overrightarrow{a}=（6，x）$，$\overrightarrow{b}$=（2，-2），且（$\overrightarrow{a}-\overrightarrow{b}$）$⊥\overrightarrow{b}$，则x的值是（　　）
A．4B．-4C．2D．-2
8．点A∈α，B∉α，C∉α，则平面ABC与平面α的位置关系是相交．
15．如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，若AP=1，AD=$\sqrt{3}$，三棱锥P-ABD的体积V=$\frac{\sqrt{3}}{4}$，则A到平面PBC的距离是$\frac{3\sqrt{13}}{13}$．
5．在△ABC中，角A，B，C的对边分别为a、b、c，tanC=$\frac{sinA+sinB}{cosA+cosB}$．
（1）求角C的大小；
（2）若△ABC的外接圆直径为1，求△ABC面积S的取值范围．
12．已知某物体的温度θ（单位：摄氏度）随时间t（单位：分钟）的变化规律：θ=m•2t+2•$\frac{1}{{2}^{t}}$ （t≥0，并且m＞0）．
（1）如果m=2，求经过多少时间，物体的温度为5摄氏度；
（2）若物体的温度总不低于2摄氏度，求m的取值范围．
9．如图所示，AB是⊙O的直径，AC切⊙O于点A，AC=AB，CO交⊙O于点P，CO的延长线交⊙O于点F，BP的延长线交AC于点E．
（1）求证：$\frac{AP}{PC}$=$\frac{FA}{AB}$；
（2）若⊙O的直径AB=1，求tan∠CPE的值．
10．设椭圆C的两个焦点分别为F1、F2，若C上存在点P满足|PF1|：|F1F2|：|PF2|=4：3：2，则C的离心率等于（　　）
A．$\frac{1}{2}$B．$\frac{2}{3}$C．$\frac{3}{4}$D．$\frac{3}{5}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网