题目内容
对向量a=(a1,a2),b=(b1,b2)定义一种运算“?”:a?b=(a1,a2)?(b1,b2)=(a1b1,a2b2).已知动点P,Q分别在曲线y=sin x和y=f(x)上运动,且 =m?
=m? +n(其中O为坐标原点),若向量m=(
+n(其中O为坐标原点),若向量m=( ,3),n=(
,3),n=( ,0),则y=f(x)的最大值为________.
,0),则y=f(x)的最大值为________.
 =m?
=m? +n(其中O为坐标原点),若向量m=(
+n(其中O为坐标原点),若向量m=( ,3),n=(
,3),n=( ,0),则y=f(x)的最大值为________.
,0),则y=f(x)的最大值为________.3
设P=(x1,y1),Q=(x,y),∵m=( ,3),
,3),
∴m? =(
=( ,3)?(x1,y1)=(
,3)?(x1,y1)=( ,3y1),
,3y1),
∵ =m?
=m? +n,∴(x,y)=(
+n,∴(x,y)=( ,3y1)+(
,3y1)+( ,0),
,0),
∴x= +
+ ,y=3y1,∴x1=2x-
,y=3y1,∴x1=2x- ,y1=
,y1= ,
,
又y1=sin x1,∴ =sin(2x-
=sin(2x- ),
),
∴y=3sin(2x- ),显然当sin(2x-
),显然当sin(2x- )=1时,y=f(x)取得最大值3.
)=1时,y=f(x)取得最大值3.
 ,3),
,3),∴m?
 =(
=( ,3)?(x1,y1)=(
,3)?(x1,y1)=( ,3y1),
,3y1),∵
 =m?
=m? +n,∴(x,y)=(
+n,∴(x,y)=( ,3y1)+(
,3y1)+( ,0),
,0),∴x=
 +
+ ,y=3y1,∴x1=2x-
,y=3y1,∴x1=2x- ,y1=
,y1= ,
,又y1=sin x1,∴
 =sin(2x-
=sin(2x- ),
),∴y=3sin(2x-
 ),显然当sin(2x-
),显然当sin(2x- )=1时,y=f(x)取得最大值3.
)=1时,y=f(x)取得最大值3.
练习册系列答案
相关题目
 ,则认为这批产品中有
,则认为这批产品中有 件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
 ,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失
,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失 元(
元( ).
). 的最大值;
的最大值; 万件,则需另投入成本
万件,则需另投入成本 (万元)。已知A产品年产量不超过80万件时,
(万元)。已知A产品年产量不超过80万件时, ;A产品年产量大于80万件时,
;A产品年产量大于80万件时, 。因设备限制,A产品年产量不超过200万件。现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完。设该厂生产A产品的年利润为L(万元)。
。因设备限制,A产品年产量不超过200万件。现已知A产品的售价为50元/件,且年内生产的A产品能全部销售完。设该厂生产A产品的年利润为L(万元)。 ;
; ,
, ,
, 的最小值为
的最小值为 .
. ,若
,若 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;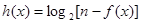 ,若此函数在定义域范围内不存在零点,求实数
,若此函数在定义域范围内不存在零点,求实数 的取值范围.[
的取值范围.[ 是定义在
是定义在 上的函数,且
上的函数,且 ,对任意
,对任意 ,若经过点
,若经过点 ,
, 的直线与
的直线与 轴的交点为
轴的交点为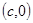 ,则称
,则称 为
为 关于函数
关于函数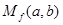 ,例如,当
,例如,当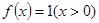 时,可得
时,可得 ,即
,即 时,
时, ;
; 当
当 时,
时, ,则当
,则当 时,
时,



 ,则
,则 =___________________.
=___________________. ,若
,若 ,则
,则 .
.