题目内容
设P为椭圆 上一点,F1,F2是其焦点.若
上一点,F1,F2是其焦点.若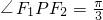 ,求△F1PF2的面积.
,求△F1PF2的面积.
解:设|PF1|=m,|PF2|=n,则 .
.
由椭圆的定义知|PF1|+|PF2|=20,即m+n=20.①
又由余弦定理得 ,即m2+n2-mn=122.②
,即m2+n2-mn=122.②
由①2-②,得 ,∴
,∴ .
.
分析:由椭圆的定义知|PF1|+|PF2|=20,即m+n=20 ①,再由余弦定理可得m2+n2-mn=122 ②,由①②求得mn的值,
代入 进行运算.
进行运算.
点评:本题考查椭圆的定义、标准方程,简单性质,以及余弦定理的应用,求出 ,是解题的关键.
,是解题的关键.
 .
.由椭圆的定义知|PF1|+|PF2|=20,即m+n=20.①
又由余弦定理得
 ,即m2+n2-mn=122.②
,即m2+n2-mn=122.②由①2-②,得
 ,∴
,∴ .
.分析:由椭圆的定义知|PF1|+|PF2|=20,即m+n=20 ①,再由余弦定理可得m2+n2-mn=122 ②,由①②求得mn的值,
代入
 进行运算.
进行运算.点评:本题考查椭圆的定义、标准方程,简单性质,以及余弦定理的应用,求出
 ,是解题的关键.
,是解题的关键. 
练习册系列答案
相关题目
 的上顶点坐标为
的上顶点坐标为 ,离心率为
,离心率为 .
. 的取值范围.
的取值范围. (a>b>0)的上顶点坐标为
(a>b>0)的上顶点坐标为 ,离心率为
,离心率为 .(Ⅰ)求椭圆C的方程;(Ⅱ)设P为椭圆上一点,A为椭圆左顶点,F为椭圆右焦点,求
.(Ⅰ)求椭圆C的方程;(Ⅱ)设P为椭圆上一点,A为椭圆左顶点,F为椭圆右焦点,求 的取值范围.
的取值范围. (a>b>0)的上顶点坐标为
(a>b>0)的上顶点坐标为 ,离心率为
,离心率为 .(Ⅰ)求椭圆C的方程;(Ⅱ)设P为椭圆上一点,A为椭圆左顶点,F为椭圆右焦点,求
.(Ⅰ)求椭圆C的方程;(Ⅱ)设P为椭圆上一点,A为椭圆左顶点,F为椭圆右焦点,求 的取值范围.
的取值范围. (a>b>0)的上顶点坐标为
(a>b>0)的上顶点坐标为 ,离心率为
,离心率为 .(Ⅰ)求椭圆C的方程;(Ⅱ)设P为椭圆上一点,A为椭圆左顶点,F为椭圆右焦点,求
.(Ⅰ)求椭圆C的方程;(Ⅱ)设P为椭圆上一点,A为椭圆左顶点,F为椭圆右焦点,求 的取值范围.
的取值范围.