题目内容
已知 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,则
,则 ,在
,在 上所有零点之和为( )
上所有零点之和为( )
| A.7 | B.8 | C.9 | D.10 |
B
解析试题分析:∵函数f(x)是定义在R上的奇函数,∴f(-x)=-f(x).又∵函数g(x)=xf(x)-1,∴g(-x)=(-x)f(-x)-1=(-x)[-f(x)]-1=xf(x)-1=g(x),∴函数g(x)是偶函数,∴函数g(x)的零点都是以相反数的形式成对出现的.∴函数g(x)在[-6,6]上所有的零点的和为0,∴函数g(x)在[-6,+∞)上所有的零点的和,即函数g(x)在(6,+∞)上所有的零点之和.由0<x≤2时,f(x)=2|x-1|-1,即 ,∴函数f(x)在(0,2]上的值域为[
,∴函数f(x)在(0,2]上的值域为[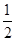 ,1],当且仅当x=2时,f(x)=1,又∵当x>2时,f(x)=
,1],当且仅当x=2时,f(x)=1,又∵当x>2时,f(x)=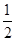 f(x-2),∴函数f(x)在(2,4]上的值域为[
f(x-2),∴函数f(x)在(2,4]上的值域为[ ],函数f(x)在(4,6]上的值域为[
],函数f(x)在(4,6]上的值域为[ ],函数f(x)在(6,8]上的值域为[
],函数f(x)在(6,8]上的值域为[ ],当且仅当x=8时,f(x)=
],当且仅当x=8时,f(x)= ,函数f(x)在(8,10]上的值域为[
,函数f(x)在(8,10]上的值域为[ ],当且仅当x=10时,f(x)=
],当且仅当x=10时,f(x)= ,故f(x)<
,故f(x)< 在(8,10]上恒成立,g(x)=xf(x)-1在(8,10]上无零点,同理g(x)=xf(x)-1在(10,12]上无零点,依此类推,函数g(x)在(8,+∞)无零点,综上函数g(x)=xf(x)-1在[-6,+∞)上的所有零点之和为8,故选B
在(8,10]上恒成立,g(x)=xf(x)-1在(8,10]上无零点,同理g(x)=xf(x)-1在(10,12]上无零点,依此类推,函数g(x)在(8,+∞)无零点,综上函数g(x)=xf(x)-1在[-6,+∞)上的所有零点之和为8,故选B
考点:本题考查了函数的零点及性质
点评:此类问题综合了函数的奇偶性,函数的零点,函数的图象和性质,难度较大,故可以用归纳猜想的方法进行处理

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案已知a是函数 的零点,
的零点,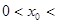 a,则
a,则 的值满足( )
的值满足( )
A. =0 =0 | B. >0 >0 | C. <0 <0 | D. 的符号不确定 的符号不确定 |
若函数 的一个正数零点附近的函数值用二分法计算,其参考数据如下:
的一个正数零点附近的函数值用二分法计算,其参考数据如下:
| f (1) = -2 | f (1.5) = 0.625 | f (1.25) = -0.984 |
| f (1.375) = -0.260 | f (1.4375) = 0.162 | f (1.40625) = -0.054 |
 的一个近似根(精确到0.1)为( )
的一个近似根(精确到0.1)为( )A.1.2 B.1.3 C.1.4 D.1.5
已知函数 的定义域为R,当
的定义域为R,当 时,
时,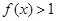 ,且对任意的实数
,且对任意的实数 R,等式
R,等式 成立.若数列
成立.若数列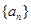 满足
满足 ,且
,且
( N*),则
N*),则 的值为( )
的值为( )
| A.4024 | B.4023 | C.4022 | D.4021 |
设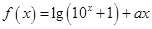 是偶函数,那么
是偶函数,那么 的值为( )
的值为( )
| A.1 | B.-1 | C.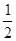 | D.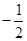 |
若函数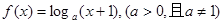 的定义域和值域都是[0,1],则a=( )
的定义域和值域都是[0,1],则a=( )
A. | B.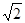 | C.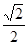 | D.2 |
 的部分图象,其中
的部分图象,其中 ,则下列所给图象中可能正确的是 ( )
,则下列所给图象中可能正确的是 ( )


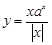
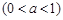 的图象的大致形状是 ( )
的图象的大致形状是 ( )