题目内容
若函数 的一个正数零点附近的函数值用二分法计算,其参考数据如下:
的一个正数零点附近的函数值用二分法计算,其参考数据如下:
| f (1) = -2 | f (1.5) = 0.625 | f (1.25) = -0.984 |
| f (1.375) = -0.260 | f (1.4375) = 0.162 | f (1.40625) = -0.054 |
 的一个近似根(精确到0.1)为( )
的一个近似根(精确到0.1)为( )A.1.2 B.1.3 C.1.4 D.1.5
C
解析试题分析:因为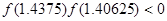 ,函数
,函数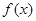 在区间
在区间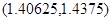 内只有一零点,且是最大的零点,故方程
内只有一零点,且是最大的零点,故方程 的一个近似根(精确到0.1)为1.4.
的一个近似根(精确到0.1)为1.4.
考点:函数的零点
点评:熟练掌握函数零点存在性定理是解题的关键,本题属于基础题.

练习册系列答案
相关题目
函数 的单调递增区间( )
的单调递增区间( )
A. | B.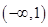 | C. | D. |
设f(x)是R上的奇函数, 且在(0, +∞)上递增, 若f( )="0," f(log4x)>0, 那么x的取值范围是( )
)="0," f(log4x)>0, 那么x的取值范围是( )
A. <x<1 <x<1 | B.x>2 |
C.x>2或 <x<1 <x<1 | D. <x<1或1<x<2 <x<1或1<x<2 |
函数 的定义域为( )
的定义域为( )
A. | B. | C. | D. |
下列结论中正确的是
| A.导数为零的点一定是极值点 |
B.如果在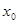 附近的左侧 附近的左侧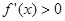 ,右侧 ,右侧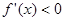 ,那么 ,那么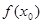 是极大值 是极大值 |
C.如果在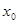 附近的左侧 附近的左侧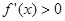 ,右侧 ,右侧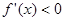 ,那么 ,那么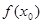 是极小值 是极小值 |
D.如果在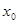 附近的左侧 附近的左侧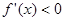 ,右侧 ,右侧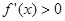 ,那么 ,那么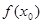 是极大值 是极大值 |
已知 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,则
,则 ,在
,在 上所有零点之和为( )
上所有零点之和为( )
| A.7 | B.8 | C.9 | D.10 |
下列函数中,既是奇函数又是区间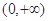 上的增函数的是( )
上的增函数的是( )
A.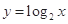 | B.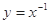 | C.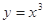 | D.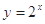 |
若定义在R上的偶函数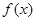 满足
满足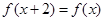 ,且当
,且当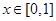 时,
时,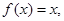 则方程
则方程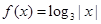 的解个数是 ( )
的解个数是 ( )
| A.0个 | B.2个 | C.4个 | D.6个 |
 的图象为折线
的图象为折线 ,设
,设 ,则函数
,则函数 的图象为( )
的图象为( )



