题目内容
已知函数
 .
.
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)若函数 在
在 处取得极值,对
处取得极值,对
 ,
, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)当 时,求证:
时,求证: .
.
(1)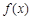 在
在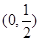 上递减,在
上递减,在 上递增;(2)
上递增;(2)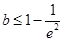 (3)
(3)
解析试题分析:(1) 时,
时,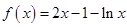 。先求导并通分整理,再令导数大于0得增区间,令导数小于0得减区间。(2)先求导,因为函数
。先求导并通分整理,再令导数大于0得增区间,令导数小于0得减区间。(2)先求导,因为函数 在
在 处取得极值,则
处取得极值,则 ,可得
,可得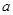 的值。对
的值。对
 ,
, 恒成立等价于
恒成立等价于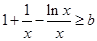 恒成立,令
恒成立,令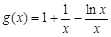 ,求导,讨论导数的符号,可得函数
,求导,讨论导数的符号,可得函数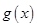 的单调性,根据单调性可得函数
的单调性,根据单调性可得函数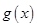 的最值,则
的最值,则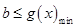 。(3)
。(3)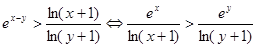 ,令
,令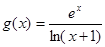 ,因为
,因为 则只要证明
则只要证明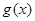 在
在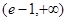 上单调递增。即证在
上单调递增。即证在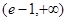 上
上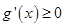 恒成立。将函数
恒成立。将函数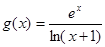 求导,分析其导数的单调性,根据其单调性求最值,证得
求导,分析其导数的单调性,根据其单调性求最值,证得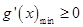 即可。
即可。
(1)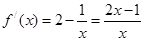
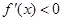 得0<x<
得0<x< ,
,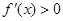 得x>
得x>
∴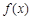 在
在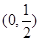 上递减,在
上递减,在 上递增.
上递增.
(2)∵函数 在
在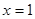 处取得极值,∴
处取得极值,∴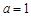 ,
,
∴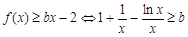 ,
,
令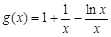 ,可得
,可得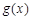 在
在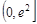 上递减,在
上递减,在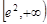 上递增,
上递增,
∴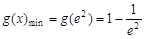 ,即
,即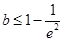 .
.
(3)证明: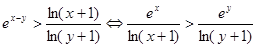 ,
,
令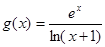 ,则只要证明
,则只要证明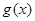 在
在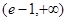 上单调递增,
上单调递增,
又∵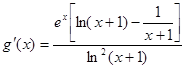 ,
,
显然函数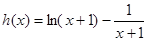 在
在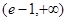 上单调递增.
上单调递增.
∴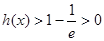 ,即
,即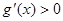 ,
,
∴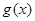 在
在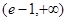 上单调递增,即
上单调递增,即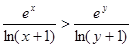 ,
,
∴当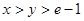 时,有
时,有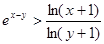 .
.
考点:1用导数研究函数的单调性及最值;2转化思想。

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
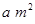 ,
,
 ,其中
,其中 .
. 的定义域
的定义域 (用区间表示);
(用区间表示); ,求
,求 的
的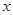 的集合(用区间表示).
的集合(用区间表示).
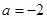 ,求证:函数
,求证:函数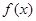 在(1,+∞)上是增函数;
在(1,+∞)上是增函数;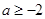 时,求函数
时,求函数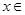 [l,e],使得
[l,e],使得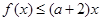 成立,求实数
成立,求实数 的取值范围.
的取值范围.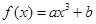 在
在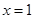 处的切线方程是
处的切线方程是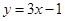 .
. 的解析式;
的解析式; 的切线方程.
的切线方程.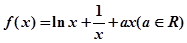
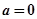 时,求
时,求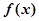 最小值;
最小值;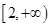 是单调减函数,求
是单调减函数,求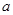 取值范围.
取值范围.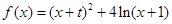 的图象在点
的图象在点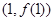 处的切线垂直于
处的切线垂直于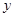 轴.
轴.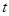 的值;
的值;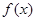 的极值.
的极值.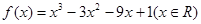 .
.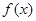 在点
在点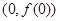 处的切线方程;
处的切线方程;