题目内容
已知函数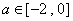 ,
, 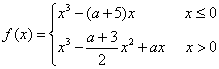 ,求证
,求证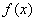 在区间
在区间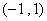 内单调递减, 在区间
内单调递减, 在区间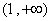 内单调递增.
内单调递增.
【证明】(1)当 时
时 ,
,
由于 ,
, ,
,
而 不恒成立所以函数
不恒成立所以函数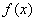 在区间
在区间 内单调递减.
内单调递减.
(2) 当 时
时 ,
,
由于 所以
所以
当 时,
时, ;当
;当 时,
时, .
.
从而函数 在区间
在区间 内单调递减,在区间
内单调递减,在区间 内单调递增.
内单调递增.
综合(1)(2),可知函数 在区间
在区间 内单调递减,在区间
内单调递减,在区间 内单调递增.
内单调递增.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
题目内容
已知函数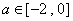 ,
, 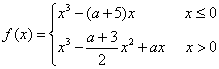 ,求证
,求证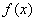 在区间
在区间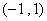 内单调递减, 在区间
内单调递减, 在区间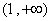 内单调递增.
内单调递增.
【证明】(1)当 时
时 ,
,
由于 ,
, ,
,
而 不恒成立所以函数
不恒成立所以函数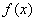 在区间
在区间 内单调递减.
内单调递减.
(2) 当 时
时 ,
,
由于 所以
所以
当 时,
时, ;当
;当 时,
时, .
.
从而函数 在区间
在区间 内单调递减,在区间
内单调递减,在区间 内单调递增.
内单调递增.
综合(1)(2),可知函数 在区间
在区间 内单调递减,在区间
内单调递减,在区间 内单调递增.
内单调递增.

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案