题目内容
已知纯虚数z满足(1+i)z=2m+i,其中i是虚数单位,则实数m的值等于 .
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:利用复数代数形式的乘除运算,可求得z=
=
,利用z为纯虚数即可求得答案.
| 2m+i |
| 1+i |
| 2m+1+(1-2m)i |
| 2 |
解答:
解:(1+i)z=2m+i,
∴z=
=
=
,又z为纯虚数,
∴2m+1=0且1-2m≠0,
解得:m=-
,
故答案为:-
.
∴z=
| 2m+i |
| 1+i |
| (2m+i)(1-i) |
| (1+i)(1-i) |
| 2m+1+(1-2m)i |
| 2 |
∴2m+1=0且1-2m≠0,
解得:m=-
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:本题考查复数代数形式的乘除运算与纯虚数的概念,属于基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
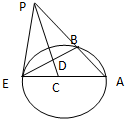 如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线分别与AE、BE相交于C、D,若∠AEB=40°,则∠PCE等于
如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线分别与AE、BE相交于C、D,若∠AEB=40°,则∠PCE等于