题目内容
离心率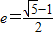 的椭圆称为“优美椭圆”,a,b,c分别表示椭圆的长半轴长,短半轴长,半焦距长,则满足“优美椭圆”的是( )
的椭圆称为“优美椭圆”,a,b,c分别表示椭圆的长半轴长,短半轴长,半焦距长,则满足“优美椭圆”的是( )A.b是a,c的等差中项
B.b是a,c的等比中项
C.2b是a,c的等差中项
D.b是a,4c的等比中项
【答案】分析:通过椭圆的离心率,构造离心率的方程,然后推出a、b、c的关系,即可得到选项.
解答:解:因为离心率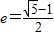 的椭圆称为“优美椭圆”,
的椭圆称为“优美椭圆”,
所以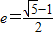 是方程e2+e-1=0的正跟,
是方程e2+e-1=0的正跟,
即有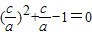 ,
,
可得c2+ac-a2=0,又c2=a2-b2,
所以b2=ac.
即b是a,c的等比中项.
故选B.
点评:本题考查椭圆的简单性质的应用,构造法是解得本题的关键,考查计算能力.
解答:解:因为离心率
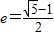 的椭圆称为“优美椭圆”,
的椭圆称为“优美椭圆”,所以
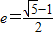 是方程e2+e-1=0的正跟,
是方程e2+e-1=0的正跟,即有
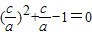 ,
,可得c2+ac-a2=0,又c2=a2-b2,
所以b2=ac.
即b是a,c的等比中项.
故选B.
点评:本题考查椭圆的简单性质的应用,构造法是解得本题的关键,考查计算能力.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
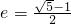 的椭圆称为“优美椭圆”,a,b,c分别表示椭圆的长半轴长,短半轴长,半焦距长,则满足“优美椭圆”的是
的椭圆称为“优美椭圆”,a,b,c分别表示椭圆的长半轴长,短半轴长,半焦距长,则满足“优美椭圆”的是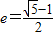 的椭圆称为“优美椭圆”,a,b,c分别表示椭圆的长半轴长,短半轴长,半焦距长,则满足“优美椭圆”的是( )
的椭圆称为“优美椭圆”,a,b,c分别表示椭圆的长半轴长,短半轴长,半焦距长,则满足“优美椭圆”的是( ) 的椭圆称为“优美椭圆”,a,b,c分别表示椭圆的长半轴长,短半轴长,半焦距长,则满足“优美椭圆”的是( )
的椭圆称为“优美椭圆”,a,b,c分别表示椭圆的长半轴长,短半轴长,半焦距长,则满足“优美椭圆”的是( )