题目内容
离心率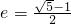
的椭圆称为“优美椭圆”，a，b，c分别表示椭圆的长半轴长，短半轴长，半焦距长，则满足“优美椭圆”的是
- A.b是a，c的等差中项
- B.b是a，c的等比中项
- C.2b是a，c的等差中项
- D.b是a，4c的等比中项
B
分析：通过椭圆的离心率，构造离心率的方程，然后推出a、b、c的关系，即可得到选项．
解答：因为离心率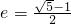的椭圆称为“优美椭圆”，
所以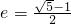是方程e2+e-1=0的正跟，
即有
，
可得c2+ac-a2=0，又c2=a2-b2，
所以b2=ac．
即b是a，c的等比中项．
故选B．
点评：本题考查椭圆的简单性质的应用，构造法是解得本题的关键，考查计算能力．
分析：通过椭圆的离心率，构造离心率的方程，然后推出a、b、c的关系，即可得到选项．
解答：因为离心率
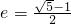的椭圆称为“优美椭圆”，所以
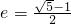是方程e2+e-1=0的正跟，即有
，可得c2+ac-a2=0，又c2=a2-b2，
所以b2=ac．
即b是a，c的等比中项．
故选B．
点评：本题考查椭圆的简单性质的应用，构造法是解得本题的关键，考查计算能力．
练习册系列答案
阅读快车系列答案
相关题目
我们把离心率等于黄金比例
的椭圆称为“优美椭圆”．设
+
=1(a＞b＞0)是优美椭圆，F、A分别是它的左焦点和右顶点，B是它的短轴的一个端点，则∠ABF等于（ ）
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| A、60° | B、75° |
| C、120° | D、90° |
离心率为黄金比
的椭圆称为“优美椭圆”．设
+
=1(a＞b＞0)是优美椭圆，F、A分别是它的左焦点和右顶点，B是它的短轴的一个顶点，则∠FBA等于（ ）
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| A、60° | B、75° |
| C、90° | D、120° |
如图，椭圆的中心在坐标原点，F为左焦点，A、B分别为长轴和短轴上的一个顶点，当FB⊥AB时，此类椭圆称为“优美椭圆”；类比“优美椭圆”，可推出“优美双曲线”的离心率为