题目内容
已知函数f(x)=tan(3x+
)
(1)求f(
)的值;
(2)设α∈(π,
),若f(
+
)=2,
①求cos(α-
)的值;
②求
的值.
| π |
| 4 |
(1)求f(
| π |
| 9 |
(2)设α∈(π,
| 3π |
| 2 |
| α |
| 3 |
| π |
| 4 |
①求cos(α-
| π |
| 4 |
②求
| 3cos2α+sin2α |
| 1-sinαcosα |
分析:(1)利用两角和的正切即可求得f(
)的值;
(2)①依题意,易求tanα=2,α∈(π,
),可求得cosα与sinα,利用两角差的余弦即可求得cos(α-
)的值;
②由tanα=2,将所求关系式中的“弦”化“切”即可求得答案.
| π |
| 9 |
(2)①依题意,易求tanα=2,α∈(π,
| 3π |
| 2 |
| π |
| 4 |
②由tanα=2,将所求关系式中的“弦”化“切”即可求得答案.
解答:解:(1)∵f(x)=tan(3x+
),
∴f(
)=tan(
+
)=
=
=-2-
;
(2)①∵f(
+
)=tan[3(
+
)+
]=tan(α+π)=tanα=2,
又α∈(π,
),
∴cosα=-
=-
,sinα=-
=-
,
∴cos(α-
)=cosαcos
+sinαsin
=-
×
-
×
=-
.
②∵tanα=2,
∴原式=
=
=
=-
.
| π |
| 4 |
∴f(
| π |
| 9 |
| π |
| 3 |
| π |
| 4 |
tan
| ||||
1-tan
|
| ||
1-
|
| 3 |
(2)①∵f(
| α |
| 3 |
| π |
| 4 |
| α |
| 3 |
| π |
| 4 |
| π |
| 4 |
又α∈(π,
| 3π |
| 2 |
∴cosα=-
| 1 | ||
|
| ||
| 5 |
| 2 | ||
|
2
| ||
| 5 |
∴cos(α-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| 5 |
| ||
| 2 |
2
| ||
| 5 |
| ||
| 2 |
3
| ||
| 10 |
②∵tanα=2,
∴原式=
| 3cos2α-2sin2α |
| sin2α+cos2α-sinαcosα |
| 3-tan2α |
| tan2α-tanα+1 |
| 3-4 |
| 4-2+1 |
| 1 |
| 3 |
点评:本题考查三角函数中的恒等变换,着重考查两角和的正切,两角差的余弦,考查转化思想与运算能力,属于中档题.

练习册系列答案
相关题目
 -1)+lnx,t为常数,且t>0.
-1)+lnx,t为常数,且t>0.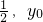 )处的切线方程为2x+y-2+ln2,求t和y0的值;
)处的切线方程为2x+y-2+ln2,求t和y0的值; -1)+lnx,t为常数,且t>0.
-1)+lnx,t为常数,且t>0. )处的切线方程为2x+y-2+ln2,求t和y的值;
)处的切线方程为2x+y-2+ln2,求t和y的值;