题目内容
已知数列 单调递增,且各项非负,对于正整数
单调递增,且各项非负,对于正整数 ,若任意的
,若任意的 ,
, (
( ≤
≤ ≤
≤ ≤
≤ ),
), 仍是
仍是 中的项,则称数列
中的项,则称数列 为“
为“ 项可减数列”.
项可减数列”.
(1)已知数列 是首项为2,公比为2的等比数列,且数列
是首项为2,公比为2的等比数列,且数列 是“
是“ 项可减数
项可减数
列”,试确定 的最大值;
的最大值;
(2)求证:若数列 是“
是“ 项可减数列”,则其前
项可减数列”,则其前 项的和
项的和 ;
;
(3)已知 是各项非负的递增数列,写出(2)的逆命题,判断该逆命题的真假,
是各项非负的递增数列,写出(2)的逆命题,判断该逆命题的真假,
并说明理由.
 单调递增,且各项非负,对于正整数
单调递增,且各项非负,对于正整数 ,若任意的
,若任意的 ,
, (
( ≤
≤ ≤
≤ ≤
≤ ),
), 仍是
仍是 中的项,则称数列
中的项,则称数列 为“
为“ 项可减数列”.
项可减数列”.(1)已知数列
 是首项为2,公比为2的等比数列,且数列
是首项为2,公比为2的等比数列,且数列 是“
是“ 项可减数
项可减数列”,试确定
 的最大值;
的最大值;(2)求证:若数列
 是“
是“ 项可减数列”,则其前
项可减数列”,则其前 项的和
项的和 ;
;(3)已知
 是各项非负的递增数列,写出(2)的逆命题,判断该逆命题的真假,
是各项非负的递增数列,写出(2)的逆命题,判断该逆命题的真假,并说明理由.
(1)2 (2) . (3)(2)的逆命题为:已知数列
. (3)(2)的逆命题为:已知数列 为各项非负的递增数列,若其前
为各项非负的递增数列,若其前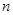 项的和满足
项的和满足 ,则该数列一定是“
,则该数列一定是“ 项可减数列”,该逆命题为真命题.
项可减数列”,该逆命题为真命题.
 . (3)(2)的逆命题为:已知数列
. (3)(2)的逆命题为:已知数列 为各项非负的递增数列,若其前
为各项非负的递增数列,若其前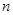 项的和满足
项的和满足 ,则该数列一定是“
,则该数列一定是“ 项可减数列”,该逆命题为真命题.
项可减数列”,该逆命题为真命题. (1)根据题意可知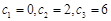 ,
,
易得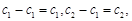
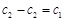 ,即数列
,即数列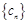 一定是“2项可减数列”.
一定是“2项可减数列”.
(2)因为数列 是“
是“ 项可减数列”,
项可减数列”,
所以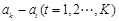 必定是数列
必定是数列 中的项.
中的项.
而 是递增数列,故
是递增数列,故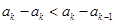
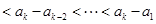 ,
,
所以必有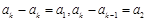 ,
,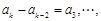
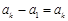 ,
,
是解决本小题的关键.
(3) 的逆命题为:
已知数列 为各项非负的递增数列,若其前
为各项非负的递增数列,若其前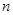 项的和满足
项的和满足 ,
,
则该数列一定是“ 项可减数列”,该逆命题为真命题.
项可减数列”,该逆命题为真命题.
证明要注意利用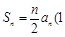 ≤
≤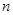 ≤
≤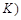 ,求出
,求出 的通项公式.
的通项公式.
(1)设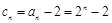 ,则
,则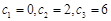 ,
,
易得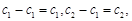
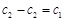 ,即数列
,即数列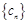 一定是“2项可减数列”,
一定是“2项可减数列”,
但因为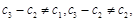
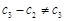 ,所以
,所以 的最大值为2. ………………5分
的最大值为2. ………………5分
(2)因为数列 是“
是“ 项可减数列”,
项可减数列”,
所以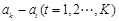 必定是数列
必定是数列 中的项, ………………………7分
中的项, ………………………7分
而 是递增数列,故
是递增数列,故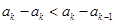
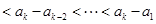 ,
,
所以必有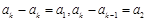 ,
,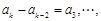
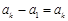 ,
,
则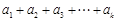
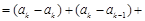
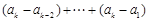
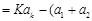
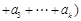 ,
,
所以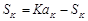 ,即
,即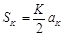 .
.
又由定义知,数列 也是“
也是“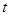 项可减数列”
项可减数列”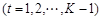 ,
,
所以 . ……………………………10分
. ……………………………10分
(3)(2)的逆命题为:
已知数列 为各项非负的递增数列,若其前
为各项非负的递增数列,若其前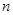 项的和满足
项的和满足 ,
,
则该数列一定是“ 项可减数列”,该逆命题为真命题.……………………12分
项可减数列”,该逆命题为真命题.……………………12分
理由如下:因为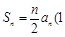 ≤
≤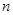 ≤
≤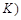 ,所以当
,所以当 ≥
≥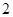 时,
时,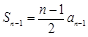 ,
,
两式相减,得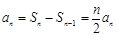
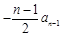 ,即
,即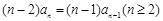 (
(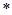 )
)
则当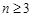 时,有
时,有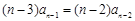 (
( )
)
由(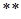 )-(
)-(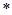 ),得
),得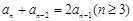 ,
,
又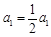 ,所以
,所以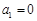 ,故数列
,故数列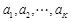 是首项为0的递增等差数列.
是首项为0的递增等差数列.
设公差为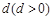 ,则
,则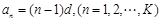 ,
,
对于任意的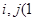 ≤
≤ ≤
≤ ≤
≤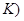 ,
,
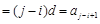 ,
,
因为 ≤
≤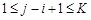 ,所以
,所以 仍是
仍是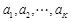 中的项,
中的项,
故数列 是“
是“ 项可减数列”.
项可减数列”.
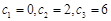 ,
,易得
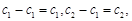
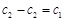 ,即数列
,即数列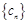 一定是“2项可减数列”.
一定是“2项可减数列”.(2)因为数列
 是“
是“ 项可减数列”,
项可减数列”,所以
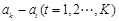 必定是数列
必定是数列 中的项.
中的项.而
 是递增数列,故
是递增数列,故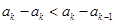
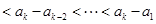 ,
,所以必有
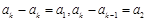 ,
,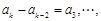
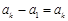 ,
,是解决本小题的关键.
(3) 的逆命题为:
已知数列
 为各项非负的递增数列,若其前
为各项非负的递增数列,若其前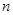 项的和满足
项的和满足 ,
,则该数列一定是“
 项可减数列”,该逆命题为真命题.
项可减数列”,该逆命题为真命题.证明要注意利用
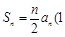 ≤
≤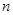 ≤
≤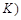 ,求出
,求出 的通项公式.
的通项公式.(1)设
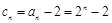 ,则
,则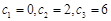 ,
,易得
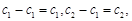
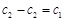 ,即数列
,即数列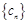 一定是“2项可减数列”,
一定是“2项可减数列”,但因为
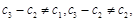
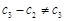 ,所以
,所以 的最大值为2. ………………5分
的最大值为2. ………………5分(2)因为数列
 是“
是“ 项可减数列”,
项可减数列”,所以
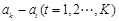 必定是数列
必定是数列 中的项, ………………………7分
中的项, ………………………7分而
 是递增数列,故
是递增数列,故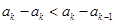
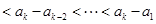 ,
,所以必有
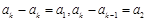 ,
,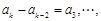
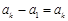 ,
,则
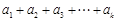
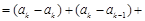
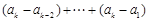
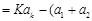
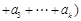 ,
,所以
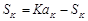 ,即
,即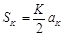 .
.又由定义知,数列
 也是“
也是“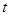 项可减数列”
项可减数列”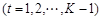 ,
,所以
 . ……………………………10分
. ……………………………10分(3)(2)的逆命题为:
已知数列
 为各项非负的递增数列,若其前
为各项非负的递增数列,若其前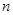 项的和满足
项的和满足 ,
,则该数列一定是“
 项可减数列”,该逆命题为真命题.……………………12分
项可减数列”,该逆命题为真命题.……………………12分理由如下:因为
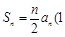 ≤
≤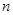 ≤
≤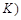 ,所以当
,所以当 ≥
≥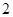 时,
时,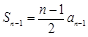 ,
,两式相减,得
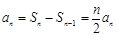
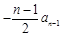 ,即
,即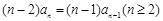 (
(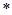 )
)则当
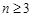 时,有
时,有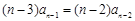 (
(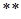 )
)由(
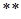 )-(
)-(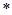 ),得
),得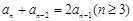 ,
,又
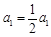 ,所以
,所以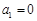 ,故数列
,故数列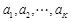 是首项为0的递增等差数列.
是首项为0的递增等差数列.设公差为
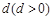 ,则
,则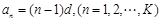 ,
,对于任意的
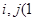 ≤
≤ ≤
≤ ≤
≤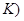 ,
,
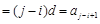 ,
,因为
 ≤
≤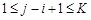 ,所以
,所以 仍是
仍是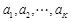 中的项,
中的项,故数列
 是“
是“ 项可减数列”.
项可减数列”.
练习册系列答案
相关题目
 ,过点
,过点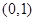 的直线
的直线 的倾斜角为
的倾斜角为 ,且
,且 ,则下列选项不正确的是( )
,则下列选项不正确的是( ) 成等差数列
成等差数列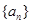 为等差数列,
为等差数列, 为正项等比数列,公比q≠1,若
为正项等比数列,公比q≠1,若 ,则( )
,则( )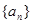 是等差数列,其中
是等差数列,其中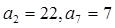 (1).求
(1).求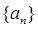 的通项;
的通项; 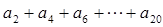 值;(3)设数列
值;(3)设数列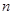 项和为
项和为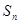 ,求
,求 是等差数列,
是等差数列, ,
, ,则
,则 等于( )
等于( ) ,
,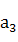 ,
,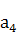 成等比数列,则
成等比数列,则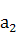 等于( )
等于( )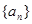 为等差数列,若
为等差数列,若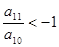 ,且它们的前
,且它们的前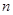 项和
项和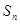 有最大值,则使
有最大值,则使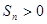 的
的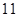
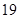
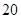
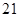
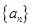 中,前15项的和
中,前15项的和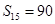 ,
, 为( )
为( )