题目内容
若函数f（x）=（x2+bx+c）e-x在（-∞，-1），（1，+∞）上单调递减，在（-1，1）上单调递增，则b+c的值为
- A.3
- B.-1
- C.1
- D.-3
A
分析：因为函数的极值点是函数增减区间的分界点，函数f（x）=（x2+bx+c）e-x在（-∞，-1），（1，+∞）上单调递减，在（-1，1）上单调递增，所以函数在x=-1处有极小值，在x=1处有极大值，而函数极值点处导数等于0，所以当x=-1和1时，导数等于0，就可解出b，c的值．
解答：f′（x）=（2x+b）e-x-（x2+bx+c）e-x
函数f（x）=（x2+bx+c）e-x在（-∞，-1），（1，+∞）上单调递减，在（-1，1）上单调递增，
∴函数在x=-1处有极小值，在x=1处有极大值
∴f′（-1）=0，f′（1）=0
即（-2+b）e-（1-b+c）e=0，（2+b）
-（1+b+c）=0
∴2b-c-3=0，1-c=0
解得b=2，c=1，∴b+c=3
故选A
点评：本题主要考查了函数极值与单调区间的关系，以及利用导数求函数极值的方法．
分析：因为函数的极值点是函数增减区间的分界点，函数f（x）=（x2+bx+c）e-x在（-∞，-1），（1，+∞）上单调递减，在（-1，1）上单调递增，所以函数在x=-1处有极小值，在x=1处有极大值，而函数极值点处导数等于0，所以当x=-1和1时，导数等于0，就可解出b，c的值．
解答：f′（x）=（2x+b）e-x-（x2+bx+c）e-x
函数f（x）=（x2+bx+c）e-x在（-∞，-1），（1，+∞）上单调递减，在（-1，1）上单调递增，
∴函数在x=-1处有极小值，在x=1处有极大值
∴f′（-1）=0，f′（1）=0
即（-2+b）e-（1-b+c）e=0，（2+b）
-（1+b+c）=0∴2b-c-3=0，1-c=0
解得b=2，c=1，∴b+c=3
故选A
点评：本题主要考查了函数极值与单调区间的关系，以及利用导数求函数极值的方法．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
若函数 f（x）＝a x (a＞0，a≠1 ) 的部分对应值如表：
| x | －2 | 0 |
| f（x） | 0.592 | 1 |
则不等 式f－1（│x│＜0）的解集是 （）
A. {x│－1＜x＜1} B. {x│x＜－1或x＞1}
C. {x│0＜x＜1} D. {x│－1＜x＜0或0＜x＜1}
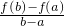（x-a）|≤T（T为常数）成立，则称函数f（x）在[a，b]上具有“T级线性逼近”．下列函数中：
；
级线性逼近”的函数的个数为
（x-a）|≤T（T为常数）成立，则称函数f（x）在[a，b]上具有“T级线性逼近”．下列函数中：
；
级线性逼近”的函数的个数为（ ）