题目内容
本题满分15分)已知函数![]() (a-b)
(a-b)![]() <b)。
<b)。
(I)当a=1,b=2时,求曲线![]() 在点(2,
在点(2,![]() )处的切线方程。
)处的切线方程。
(II)设![]() 是
是![]() 的两个极值点,
的两个极值点,![]() 是
是![]() 的一个零点,且
的一个零点,且![]() ,
,![]()
证明:存在实数![]() ,使得
,使得![]() 按某种顺序排列后的等差数列,并求
按某种顺序排列后的等差数列,并求![]()
解析:本题主要考查函数的极值概念、导数运算法则、切线方程、导线应用、等差数列等基础知识,同时考查抽象概括、推理论证能力和创新意识。
(Ⅰ)解:当a=1,b=2时,
因为f’(x)=(x-1)(3x-5)
故f’(2)=1
f(2)=0,
所以f(x)在点(2,0)处的切线方程为y=x-2
(Ⅱ)证明:因为f′(x)=3(x-a)(x-![]() ),
),
由于a<b.
故a<![]() .
.
所以f(x)的两个极值点为x=a,x=![]() .[
.[
不妨设x1=a,x2=![]() ,
,
因为x3≠x1,x3≠x2,且x3是f(x)的零点,
故x3=b.
又因为![]() -a=2(b-
-a=2(b-![]() ),
),
x4=![]() (a+
(a+![]() )=
)=![]() ,
,
所以a,![]() ,
,![]() ,b依次成等差数列,
,b依次成等差数列,
所以存在实数x4满足题意,且x4=![]() .
.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 ,曲线
,曲线
 且直线与曲线恰有三个公共点时,求实数
且直线与曲线恰有三个公共点时,求实数 的取值;
的取值; ,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。[来源:Z+xx+k.Com]
,直线与曲线M的交点依次为A,B,C,D四点,求|AB+|CD|的取值范围。[来源:Z+xx+k.Com]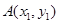 ,
, 是抛物线
是抛物线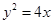 上相异两点,且满足
上相异两点,且满足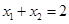 .
. 的中垂线经过点
的中垂线经过点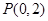 ,求直线
,求直线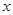 轴于点
轴于点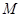 ,求
,求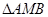 的面积的最大值及此时直线
的面积的最大值及此时直线 在[1,+∞)上为增函数,且
在[1,+∞)上为增函数,且 ,
, 的值;
的值; 在[1,+∞)上为单调函数,求实数
在[1,+∞)上为单调函数,求实数 的取值范围;
的取值范围; 上至少存在一个
上至少存在一个 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围. 为
为 上的奇函数,当
上的奇函数,当 时,
时, ,不等式组
,不等式组 的解集是
的解集是 .
. 的方程:
的方程:
 根的个数
根的个数
 ,
, ,若
,若 ,求实数m的取值范围
,求实数m的取值范围