Question

（本题满分15分）

已知点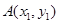，是抛物线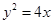上相异两点，且满足．

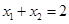（Ⅰ）若的中垂线经过点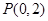，求直线的方程；

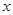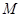（Ⅱ）若的中垂线交轴于点，求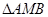的面积的最大值及此时直线的方程．

 

Answer 1

【答案】

（Ⅰ）；（Ⅱ），直线方程为。

【解析】

试题分析：（I）当垂直于轴时，显然不符合题意，

所以可设直线的方程为，代入方程得：

∴              ………………………………2分

得： 

∴直线的方程为                  

∵中点的横坐标为1，∴中点的坐标为  …………………………4分       

∴的中垂线方程为 

∵的中垂线经过点，故，得   ………………………6分

∴直线的方程为           ………………………7分

（Ⅱ）由（I）可知的中垂线方程为，∴点的坐标为……8分

因为直线的方程为

∴到直线的距离…………………10分

由 得，，

     …………………………12分

∴,  设,则，

，，由，得 

在上递增，在上递减，当时，有最大值

得：时，    

直线方程为                    ……………15分

（本题若运用基本不等式解决，也同样给分）

法二：

（Ⅰ）当垂直于轴时，显然不符合题意，

当不垂直于轴时，根据题意设的中点为，

则                    …………2分

由、两点得中垂线的斜率为，    ………………4分

由，得                   ………………6分

∴直线的方程为                ……………7分

（Ⅱ）由（Ⅰ）知直线的方程为          ………………8分

中垂线方程为，中垂线交轴于点

点到直线的距离为       ………………10分

由得：

     

当时，有最大值，此时直线方程为     ………15分；

考点：抛物线的简单性质；直线与抛物线的综合应用；中点坐标公式；直线垂直的条件。

点评：（1）本题主要考查直线与抛物线的综合应用等基础知识，考查了学生运算能力、推理论证以及分析问题、解决问题的能力，以及分类讨论、化归与转化思想．（2）做此题的关键是表示出的面积。本题在计算过程中较为复杂繁琐，我们在计算的过程中一定要耐住性子，认真、细致，避免出现计算错误。