题目内容
【题目】设![]() ,
,![]()
(1)求![]() 在区间
在区间![]() 上的值域;
上的值域;
(2)求![]() 在区间
在区间![]() 上的值域:
上的值域:
(3)已知![]() ,若对于任意
,若对于任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)见详解 (3)
(2)见详解 (3)![]()
【解析】
(1) 根据题意,判断出![]() 在
在![]() 上的单调性,即可求出
上的单调性,即可求出![]() 在区间
在区间![]() 上的值域;
上的值域;
(2) 根据题意,先求出![]() 的对称轴,再根据区间
的对称轴,再根据区间![]() 与对称轴的位置关系进行分类讨论,即可求出
与对称轴的位置关系进行分类讨论,即可求出![]() 在区间
在区间![]() 上的值域;
上的值域;
(3) 根据题意,只需满足![]() 在区间
在区间![]() 上的值域是
上的值域是![]() 在区间
在区间![]() 上的值域的子集,根据集合之间的包含关系即可求得
上的值域的子集,根据集合之间的包含关系即可求得![]() 的取值范围。
的取值范围。
(1) 根据题意,可得![]()
易知![]() 在
在![]() 上是单调递增的,
上是单调递增的,
![]()
![]()
![]() 在区间
在区间![]() 上的值域为
上的值域为![]() .
.
(2)由题意得,![]() 的对称轴为
的对称轴为![]() ,则
,则
当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增,
上单调递增,
![]() ,
,![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ;
;
当![]() 时,
时,![]() 在区间
在区间![]() 上单调递减,
上单调递减,
![]() ,
,![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ;
;
当![]() 时,
时,![]() 在区间
在区间![]() 上先减后增,
上先减后增,
![]()
若![]() ,则
,则 ![]() ,
,![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ;
;
若![]() ,则
,则 ![]() ,
,![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ;
;
若![]() ,则
,则 ![]() ,
,![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ;
;
(3) 根据(1)(2)可知,![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,当
,当![]() 时,
时,![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ;若对于任意
;若对于任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,只需满足
成立,只需满足![]() 在区间
在区间![]() 上的值域是
上的值域是![]() 在区间
在区间![]() 上的值域的子集,即
上的值域的子集,即

解得![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】抽样得到某次考试中高二年级某班![]() 名学生的数学成绩和物理成绩如下表:
名学生的数学成绩和物理成绩如下表:
学生编号 |
|
|
|
|
|
|
数学成绩 |
|
|
|
|
|
|
物里成绩 |
|
|
|
|
|
|
(1)在图中画出表中数据的散点图;
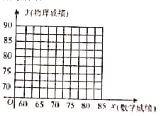
(2)建立![]() 关于
关于![]() 的回归方程:(系数保留到小数点后两位).
的回归方程:(系数保留到小数点后两位).
(3)如果某学生的数学成绩为![]() 分,预测他本次的物理成绩(成绩取整数).
分,预测他本次的物理成绩(成绩取整数).
参考公式:回归方程为![]() ,其中
,其中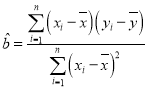 ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() .
.
【题目】某商场在促销期间规定:商场内所有商品按标价的![]() 出售,当顾客在商场内消费一定金额后,按如下方案获得相应金额的奖券:
出售,当顾客在商场内消费一定金额后,按如下方案获得相应金额的奖券:
消费金额(元)的范围 |
|
|
|
| … |
获得奖券的金额(元) | 30 | 60 | 100 | 130 | … |
根据上述促销方法,顾客在该商场购物可以获得双重优惠,例如:购买标价为400元的商品,则消费金额为320元,获得的优惠额为:![]() 元,设购买商品得到的优惠率=(购买商品获得的优惠额)/(商品标价),试问:
元,设购买商品得到的优惠率=(购买商品获得的优惠额)/(商品标价),试问:
(1)若购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)对于标价在![]() (元)内的商品,顾客购买标价为多少元的商品,可得到不小于
(元)内的商品,顾客购买标价为多少元的商品,可得到不小于![]() 的优惠率?
的优惠率?