Question

给定集合，若对于任意，都有且，则称集合为完美集合，给出下列四个论断：①集合是完美集合；②完美集合不能为单元素集；③集合为完美集合；④若集合为完美集合，则集合为完美集合．

其中正确论断的序号是                   ．

 

Answer 1

【答案】

③.

【解析】

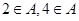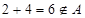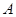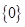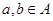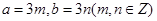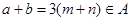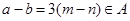试题分析：集合的创新问题，通常需要弄清题目给出的新定义、新概念、新法则与教材上的知识间的联系，将新的定义、概念、法则转化为“常规数学”问题，然后求解.①，但，故集合不是完美集合；②可以证明集合是完美集合，它是单元素集；③设，即，，，∴集合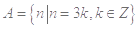为完美集合；④如集合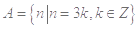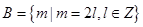，是完美集合，但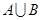不是完美集合，实际上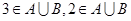，，但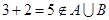．故只有③正确．

考点：集合中的新定义问题．