如图所示的几何体中.四边形ABCD为矩形.AD⊥平面.AE=EB=BC=2.F为CE上的点.且BF⊥平面ACE． (1)求证:AE∥平面BFD, (2)求三棱锥C﹣BGF的体积．题目和参考答案——青夏教育精英家教网—

题目内容

如图所示的几何体中，四边形ABCD为矩形，AD⊥平面，AE=EB=BC=2，F为CE上的点，且BF⊥平面ACE．

（1）求证：AE∥平面BFD；

（2）求三棱锥C﹣BGF的体积．

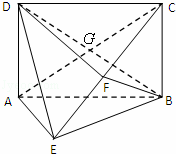
解答：（1）证明：如图，

由题意可得G是AC的中点，连接FG，

∵BF⊥平面ACE，则CE⊥BF，而BC=BE，

∴F是EC中点，

在△AEC中，FG∥AE，∴AE∥平面BFD；

（2）解：∵AE∥平面BFD，∴AE∥FG，

由题可得AE⊥平面BCE，∴FG⊥平面BCE．

∵G是AC的中点，F是CE中点，∴AE∥FG且FG=，

∵BF⊥平面ACE，∴BF⊥CE，∴Rt△BCE中，BF=，

∴，

∴=．

练习册系列答案

相关题目

如图14所示，在四棱锥P ABCD中，PA⊥底面ABCD, AD⊥AB，AB∥DC，AD＝DC＝AP＝2，AB＝1，点E为棱PC的中点．

(1)证明：BE⊥DC；

(2)求直线BE与平面PBD所成角的正弦值；

(3)若F为棱PC上一点，满足BF⊥AC，求二面角F AB P的余弦值．

图14

某射手射击所得环数X的分布列为：

X	4	5	6	7	8	9	10
P	0.02	0.04	0.06	0.09	0.28	0.29	0.22

则此射手“射击一次命中环数大于7”的概率为(　　)

A．0.28 B．0.88

C．0.79 D．0.51

若α，β是两个不同的平面，下列四个条件：

①存在一条直线a，a⊥α，a⊥β；

②存在一个平面γ，γ⊥α，γ⊥β；

③存在两条平行直线a，b，a⊂α，b⊂β，a∥β，b∥α；

④存在两条异面直线a，b，a⊂α，b⊂β，a∥β，b∥α．

那么可以是α∥β的充分条件有（　C　）

　 A． 4个 B． 3个 C． 2个 D． 1个

已知双曲线的方程为﹣x²=1，点A的坐标为（0，﹣），B是圆（x﹣）²+y²=1上的点，点M在双曲线的上支上，则|MA|+|MB|的最小值为　　　　　　．

若A（﹣2，3）、B（3，﹣2）、C（，m﹚三点在同一直线上，则m的值为（　　）

　 A． ﹣2 B． 2 C． ﹣ D．

三个球的半径之比是1：2：3　则最大球的体积是其余两个球的体积之和的（　　）

　 A． 4倍 B． 3倍 C． 2倍 D． 1倍

设a＝log₃6，b＝log₅10，c＝log₇14，则(　　)

A. c>b>a B. b>c>a C. a>c>b D. a>b>c

函数f(x)＝()^x－log₂(x＋2)在区间[－1，1]上的最大值为(　　)

A．1 B．3 C．4 D．5

试题分类