题目内容
求使函数f(x)=(a2+4a-5)x2-4(a-1)x+3的图象全在x轴上方成立的充要条件.
解:根据题意,对任意的x∈R有f(x)>0恒成立,
①若a2+4a-5=0,则a=1或a=-5,
当a=1时,f(x)=3>0恒成立,即a=1符合题意;
当a=-5时,f(x)=24x+3>0不恒成立,即a=-5不符合题意;
②若a2+4a-5≠0,
则根据题意,有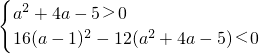 ,
,
解可得1<a<19;
综上所述,所求的充要条件为1≤a<19.
分析:根据题意,函数f(x)=(a2+4a-5)x2-4(a-1)x+3的图象全在x轴上方,即对任意的x∈R有f(x)>0恒成立;分①a2+4a-5=0与②a2+4a-5≠0两种情况讨论,分别求出a的范围,进而对求出的范围求并集可得答案.
点评:本题考查充要条件的判断,解题中要注意对a2+4a-5=0与a2+4a-5≠0分类讨论,容易遗忘a2+4a-5=0这种情况.
①若a2+4a-5=0,则a=1或a=-5,
当a=1时,f(x)=3>0恒成立,即a=1符合题意;
当a=-5时,f(x)=24x+3>0不恒成立,即a=-5不符合题意;
②若a2+4a-5≠0,
则根据题意,有
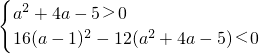 ,
,解可得1<a<19;
综上所述,所求的充要条件为1≤a<19.
分析:根据题意,函数f(x)=(a2+4a-5)x2-4(a-1)x+3的图象全在x轴上方,即对任意的x∈R有f(x)>0恒成立;分①a2+4a-5=0与②a2+4a-5≠0两种情况讨论,分别求出a的范围,进而对求出的范围求并集可得答案.
点评:本题考查充要条件的判断,解题中要注意对a2+4a-5=0与a2+4a-5≠0分类讨论,容易遗忘a2+4a-5=0这种情况.

练习册系列答案
相关题目