题目内容
已知f(x)=logax(a>0,a≠1),若对任何x∈[3,+∞),都有|f(x)|≥1成立,则a的取值范围是
- A.

- B.

- C.
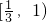
- D.(1,3]
B
分析:根据对数的图象和性质,分当a>1和0<a<1两种情况,去掉绝对值转化|f(x)|≥1,再用最值法解决.
解答:①当a>1时,对任意x∈[3,+∞),此时|f(x)|=f(x)
转化为任意x∈[3,+∞)时,都有logax≥1恒成立
即logax的最小值≥1,即loga3≥1,
∴a≤3
此时1<a≤3
②当0<a<1时,对任意x∈[3,+∞),此时|f(x)|=-f(x)
转化为任意x∈[3,+∞)时,都有-logax≥1恒成立,
即logax≤-1恒成立
即logax的最大值≤-1,即loga3≤-1,
∴此时a≥
综上a的取值范围为:[ ,1)∪(1,3]
,1)∪(1,3]
故选B
点评:本题主要考查对数函数的图象和性质的应用,涉及了图象的分布及单调性求最值来解决恒成立问题.
分析:根据对数的图象和性质,分当a>1和0<a<1两种情况,去掉绝对值转化|f(x)|≥1,再用最值法解决.
解答:①当a>1时,对任意x∈[3,+∞),此时|f(x)|=f(x)
转化为任意x∈[3,+∞)时,都有logax≥1恒成立
即logax的最小值≥1,即loga3≥1,
∴a≤3
此时1<a≤3
②当0<a<1时,对任意x∈[3,+∞),此时|f(x)|=-f(x)
转化为任意x∈[3,+∞)时,都有-logax≥1恒成立,
即logax≤-1恒成立
即logax的最大值≤-1,即loga3≤-1,
∴此时a≥

综上a的取值范围为:[
 ,1)∪(1,3]
,1)∪(1,3]故选B
点评:本题主要考查对数函数的图象和性质的应用,涉及了图象的分布及单调性求最值来解决恒成立问题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
已知f(x)是定义在R上的奇函数,当x>0时,f(x)=log
x,那么f(-
)的值是( )
| 1 |
| 4 |
| 1 |
| 2 |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |