题目内容
设函数f(x)=sin3x+acos3x(a∈R)满足f( )=f(
)=f(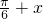 ),则a的值是
),则a的值是
- A.3
- B.2
- C.1
- D.0
D
分析:由题意可得函数f(x)的图象关于x= 对称,化简函数可得f(x)=
对称,化简函数可得f(x)= sin(3x+φ),进而由f(
sin(3x+φ),进而由f( )=±
)=± 解方程可得答案.
解方程可得答案.
解答:由可得f( )=f(
)=f(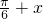 ),函数f(x)的图象关于x=
),函数f(x)的图象关于x= 对称,
对称,
又f(x)=sin3x+acos3x= (
( sin3x+
sin3x+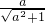 cos3x)
cos3x)
= sin(3x+φ),(其中tanφ=a),
sin(3x+φ),(其中tanφ=a),
由函数的图象可知,函数在对称轴处取到最大值或最小值,
即f( )=sin3•
)=sin3• +acos3•
+acos3• =1=±
=1=± ,即a2+1=1,解得a=0,
,即a2+1=1,解得a=0,
故选D
点评:本题考查两角和与差的正弦函数,得出函数f(x)的图象关于x= 对称是解决问题的关键,属中档题.
对称是解决问题的关键,属中档题.
分析:由题意可得函数f(x)的图象关于x=
 对称,化简函数可得f(x)=
对称,化简函数可得f(x)= sin(3x+φ),进而由f(
sin(3x+φ),进而由f( )=±
)=± 解方程可得答案.
解方程可得答案.解答:由可得f(
 )=f(
)=f(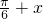 ),函数f(x)的图象关于x=
),函数f(x)的图象关于x= 对称,
对称,又f(x)=sin3x+acos3x=
 (
( sin3x+
sin3x+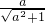 cos3x)
cos3x)=
 sin(3x+φ),(其中tanφ=a),
sin(3x+φ),(其中tanφ=a),由函数的图象可知,函数在对称轴处取到最大值或最小值,
即f(
 )=sin3•
)=sin3• +acos3•
+acos3• =1=±
=1=± ,即a2+1=1,解得a=0,
,即a2+1=1,解得a=0,故选D
点评:本题考查两角和与差的正弦函数,得出函数f(x)的图象关于x=
 对称是解决问题的关键,属中档题.
对称是解决问题的关键,属中档题. 
练习册系列答案
相关题目
设函数f(x)=sin3x+|sin3x|,则f(x)为( )
A、周期函数,最小正周期为
| ||
B、周期函数,最小正周期为
| ||
| C、周期函数,数小正周期为2π | ||
| D、非周期函数 |





