题目内容
若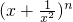 (n∈N+)的展开式中存在常数项A,此时二项式系数的最大值为B,则
(n∈N+)的展开式中存在常数项A,此时二项式系数的最大值为B,则
- A.A>B
- B.A≥B
- C.A<B
- D.A≤B
D
分析:由二项展开式的通项 =Cnrxn-3r,可知,当n-3r=0即r=
=Cnrxn-3r,可知,当n-3r=0即r= ,为常数项,即可得A=
,为常数项,即可得A= ,由二项式系数的性质可求B,然后结合二项式系数的单调性可比较A,B的大小
,由二项式系数的性质可求B,然后结合二项式系数的单调性可比较A,B的大小
解答:由题意可得, =Cnrxn-3r
=Cnrxn-3r
令n-3r=0可得r= ,则n一定是3的倍数
,则n一定是3的倍数
此时A=
当n为偶数时,二项式系数的最大值为B=
若n为奇数时,二项式系数的最大值为B=
当n=3时,A=B
当n>3时,
 ,由二项式系数的性质可知
,由二项式系数的性质可知 即B>A
即B>A
综上可得,A≤B
故选:D
点评:本题主要考查了二项式系数的性质的应用,解题中要注意对n的讨论的根本原因是要比较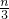 与
与 的大小,进而比较A=
的大小,进而比较A= 与B=
与B= 的大小
的大小
分析:由二项展开式的通项
 =Cnrxn-3r,可知,当n-3r=0即r=
=Cnrxn-3r,可知,当n-3r=0即r= ,为常数项,即可得A=
,为常数项,即可得A= ,由二项式系数的性质可求B,然后结合二项式系数的单调性可比较A,B的大小
,由二项式系数的性质可求B,然后结合二项式系数的单调性可比较A,B的大小解答:由题意可得,
 =Cnrxn-3r
=Cnrxn-3r令n-3r=0可得r=
 ,则n一定是3的倍数
,则n一定是3的倍数此时A=

当n为偶数时,二项式系数的最大值为B=

若n为奇数时,二项式系数的最大值为B=

当n=3时,A=B
当n>3时,

 ,由二项式系数的性质可知
,由二项式系数的性质可知 即B>A
即B>A综上可得,A≤B
故选:D
点评:本题主要考查了二项式系数的性质的应用,解题中要注意对n的讨论的根本原因是要比较
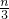 与
与 的大小,进而比较A=
的大小,进而比较A= 与B=
与B= 的大小
的大小 
练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
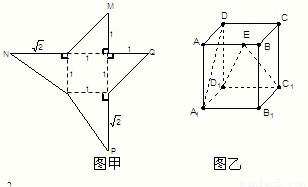
 如图某一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,BQ=BR,点S、D、A、Q共线及P、D、C、R共线.
如图某一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,BQ=BR,点S、D、A、Q共线及P、D、C、R共线. (2010•龙岩二模)图甲是一个几何体的表面展开图,图乙是棱长为1cm的正方体.
(2010•龙岩二模)图甲是一个几何体的表面展开图,图乙是棱长为1cm的正方体.